作者：Abhishek Parbhakar

翻译：老齐

与本文相关的图书推荐：《数据准备和特征工程》

本书已经发售，购买：【电子工业出版社天猫旗舰店】

信息论是对深度学习和AI有重大贡献的一个重要领域，当然，很多人对它知之甚少。如你所知，深度学习的基石是微积分、概率论和统计学，信息论可以视为是它们之间的复杂的融合。AI中的一些概念就来自于信息论或相关领域，例如：

• 常见的交叉熵和损失函数
• 基于最大信息熵的决策树
• NLP和语音处理中的Viterbi算法
• 循环神经网络和其他模型中的编码器概念

信息论简史

20世纪早期，科学家和工程师困惑于这样的问题：如何量化信息？有没有某个数学化的方法能够测量信息量？例如，以下两句话：

• Bruno是一只狗。
• Bruno是一只大个的有着棕色皮毛的狗。

不难看出，第二句告诉了我们更多的信息，狗是大的，毛是棕色的，而不仅仅告诉我们是一只狗。我们如何量化这两句话的差异？我们能用数学化的方法测量第二句比第一句有更多得信息吗？

科学家困惑于此问题。用语义或者语句的数量来衡量信息，只能让问题更麻烦。后来，数学家和工程师克劳德·香农提出了“熵”的思想，这种思想永远改变了我们的世界，标志着“数字信息时代”的开始。

香农提出“数据的语义相彼此无关”，即数据的类型和含义在涉及信息内容时则无关紧要,相反，他根据概率分布和“不确定性”对信息进行了量化。香农还引入了“位”（“bit”），并谦虚地归功于他的同事John Tukey。 这一革命性的思想不仅奠定了信息理论的基础，而且还为人工智能等领域的发展开辟了新的途径。

下面我们讨论深度学习和数据科学中4个流行的且广泛应用的、必须要知道的信息论概念：

熵

也称为信息熵或者香农熵。

初步理解

熵是度量不确定性的量，让我们设想两个实验：

1. 抛一枚均匀的硬币(P(H)=0.5)，观察它的输出，假设H
2. 投掷一枚有偏差的硬币(P(H)=0.99)，观察它的输出，假设H

比较这两个实验，相对于实验1，实验2更容易预测到它的结果。那么，我们说实验1比实验2具有更强的不确定性，实验中的这种不确定性就用熵来度量。

因此，如果实验具有更多不确定性，熵的值越大，或者说，实验结果的可预测性越强，熵越小。实验的概率分布常常用熵计算。

实验结果确定，即完全可预测，就相当于抛出一门P(H)=1的硬币，此时熵为0。如果实验完全随机，例如掷骰子，可预测性最低，具有最大的不确定，其实验的熵也最高。

另一种对熵的理解是通过观测随机实验输出的平均获得信息。从一个实验结果所获得的信息可以定义为一个概率函数，输出越少，获得信息越多。

例如，一个确定性实验，我们都知道其结果，所以，就没有获得新信息，熵即为0。

数学表示

X为离散星随机变量，其状态分别是$x_1, …, x_n$，其熵定义为：

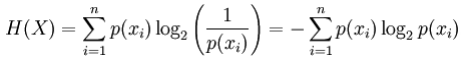
其中$p(x_i)$是X的第i个输出（状态）

应用

• 熵可用于决策树模型，构建树的每一步，利用熵对特征进行选择。
• 依据最大熵原则选择模型，即在众多候选模型中，熵最大的模型最好。

交叉熵

初步理解

交叉熵用于比较两个概率分布，通过它能够知道两个分布的相似度。

数学表示

假设p和q两个概率分布，用如下方式定义交叉熵：

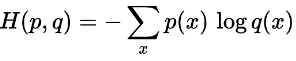
应用

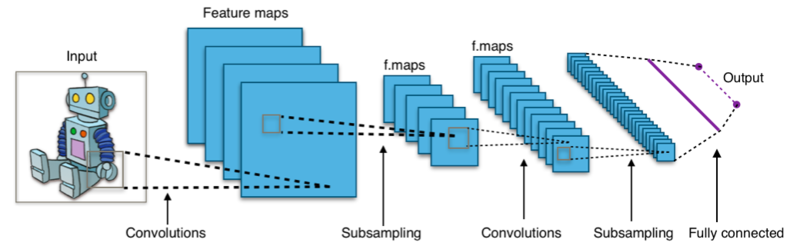
• 交叉熵损失函数广泛用于分类模型，例如logistic回归。交叉熵损失函数随着预测与真实输出的偏差而增大。
• 在深度学习中，如卷积神经网络，最后输出softmax层经常使用交叉熵损失函数。

互信息

初步理解

互信息用于度量两个概率分布或随机变量间的相互独立性，通过它可以知道一个变量的信息有多少与另一个相关。

互信息显示了随机变量之间的相关性，比单纯的线性相关系数更一般化。

数学公式

两个离散型随机变量X和Y的互信息定义为：

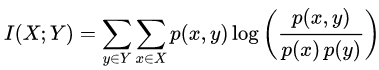
其中p(x,y)是X和Y的联合概率分布，p(x)和p(y)分别是X和Y的边际概率分布。

应用

• 特征选择：除了相关系数，还可以用互信息。相关系数仅限于线性相关，对非线性相关不适用，但是互信息则不然。零的相互独立性保证了随机变量是独立的，而零相关性则不是。
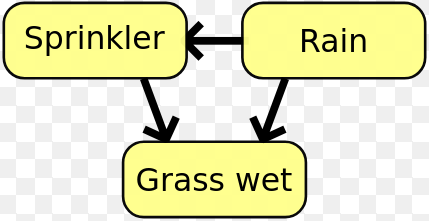
• 在贝叶斯网络总，互信息用于学习两个随机变量的之间的关系结构，并且定义这种关系的强度。

KL散度

也叫做相对熵

初步理解

KL散度是另外一种度量两个随机分布相似度的方式，它度量的是一个分布相对另外一个分布的偏差。

假设有一些数据，其真实分布是P，但P是未知的，因此我们选择一个新的分布Q，来近似该数据。 由于Q只是一个近似值，因此它严格等于P，会发生一些信息丢失，此处的信息丢失就是由KL散度度量的。

当选择的P近似于Q时，P和Q之间的KL散度显示有多少信息丢失。

数学公式

随机分布Q相对于随机分布的KL散度定义如下：

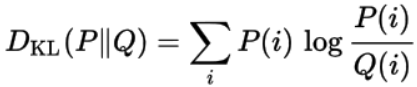
应用

KL散度常用于无监督机器学习技术变分自编码器。

信息理论最初是由数学家和电气工程师克劳德·香农（Claude Shannon）在1948年发表的开创性论文《通信的数学理论》中提出的。

原文链接：https://towardsdatascience.com/must-know-information-theory-concepts-in-deep-learning-ai-e54a5da9769d

搜索技术问答的公众号：老齐教室

在公众号中回复：老齐，可查看所有文章、书籍、课程。

觉得好看，就点赞转发