用信息论剖析深度学习
2020-04-10
作者:Lilian Weng
翻译:老齐
与本文相关书籍推荐:《数据准备和特征工程》

最近,我聆听了Naftali Tishby教授的演讲“深度学习中的信息论”,感觉很有意思。他在演讲中说明了如何将信息论用于研究深度神经网络的增长和转换,他利用IB(Information Bottleneck)方法,为深度神经网络(DNN)开创了一个新的领域,由于参数的数量成指数增长,导致传统的学习理论在该领域均行不通。另外的一种敏锐观察显示,在DNN训练中包含了两个迥异的阶段:首先,训练网络充分表示输入数据,最小化泛化误差;然后,通过压缩输入的表示形式,它学会了忘记不相关的细节。
基本概念
马尔科夫链
马尔科夫过程是一个“无记忆”(也称为“马尔科夫性质”)的随机过程,马尔科夫链是一类包含多个离散状态的马尔科夫过程,也就是说,过程的未来状态的条件概率仅由当前状态决定,而不取决于过去状态。
KL散度
KL散度用于度量一个概率分布p偏离另一个期望的概率分布q的程度,它是不对称的。
$$\begin{aligned}D_{KL}(p | q) &= \sum_x p(x) \log \frac{p(x)}{q(x)} dx \
&= - \sum_x p(x)\log q(x) + \sum_x p(x)\log p(x) \
&= H(P, Q) - H(P)\end{aligned} $$
当$p(x)$ == $q(x)$时,$D_{KL}$达到最小值零。
互信息
互信息度量两个变量之间的相互依赖程度,它把一个随机变量通过另一个随机变量所获得的“信息量”进行量化,互信息是对称的。
$$
\begin{aligned}
I(X;Y) &= D_{KL}[p(x,y) | p(x)p(y)] \
&= \sum_{x \in X, y \in Y} p(x, y) \log(\frac{p(x, y)}{p(x)p(y)}) \
&= \sum_{x \in X, y \in Y} p(x, y) \log(\frac{p(x|y)}{p(x)}) \
&= H(X) - H(X|Y) \
\end{aligned}$$
数据处理不等式(DPI)
对于任意的马尔科夫链: $X \to Y \to Z$,我们有$I(X; Y) \geq I(X; Z)$。
深度神经网络可以看作是一个马尔科夫链,因此当我们沿着DNN层向下移动时,层与输入之间的互信息只会减少。
再参数化不变性
对于两个可逆函数$\phi$,$\psi$,互信息仍然是:$I(X; Y) = I(\phi(X); \psi(Y))$。
例如,如果我们在DNN的一个层中调整权重,它不会影响这个层和另一个层之间的互信息。
马尔科夫链的深度神经网络
训练数据来自$X$和$Y$联合分布的抽样观测,输入变量$X$和隐藏层的权重都是高维随机变量。真实值$Y$和预测值$\hat{Y}$是分类设置中较小维度的随机变量。
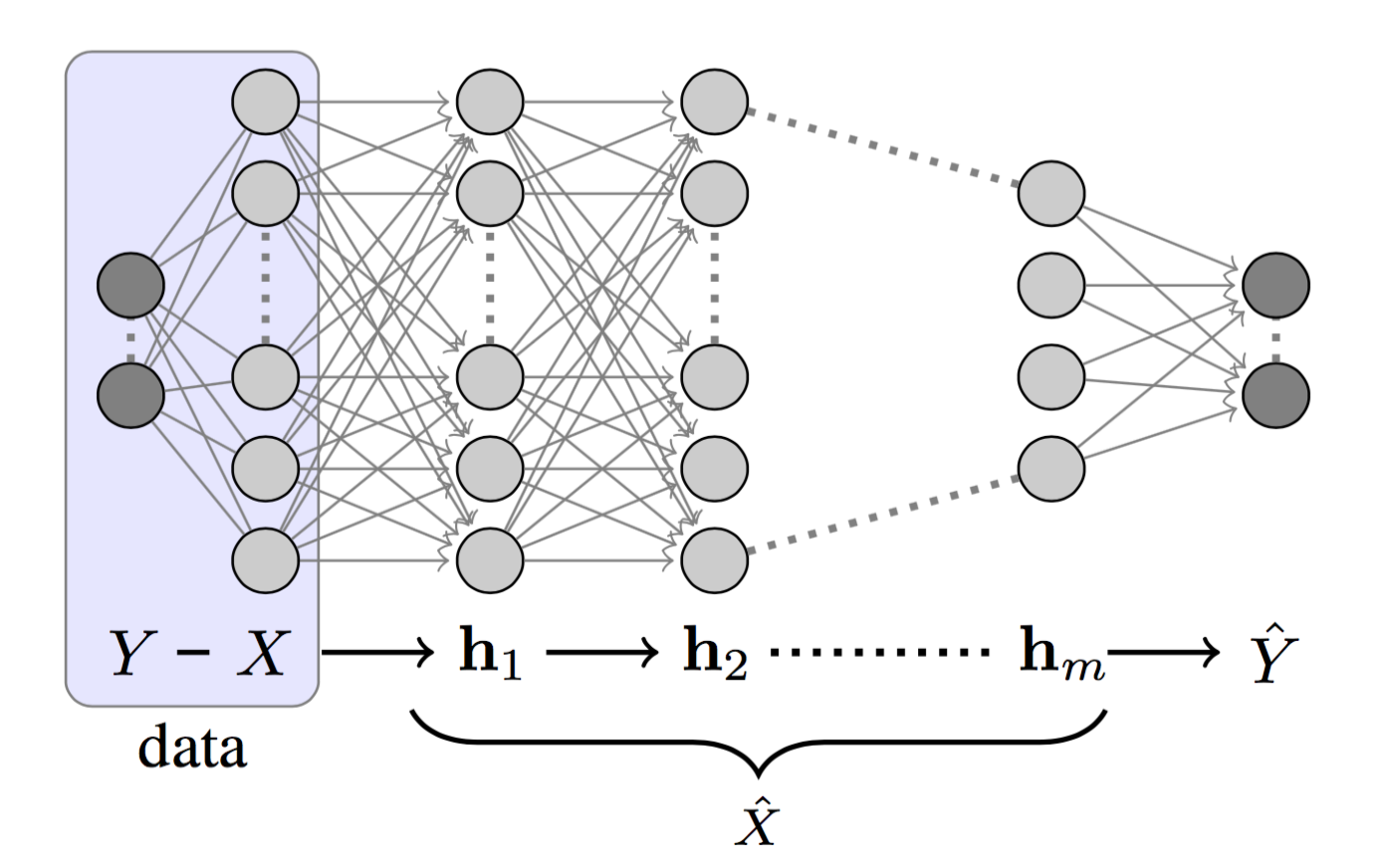
图1:一个深度神经网络的结构,它包含标签$Y$、输入层$X$、隐藏层$h_1、…、h_m$和预测值$\hat{Y}$。
如果我们将DNN的隐藏层标记为$h_1,h_2,…,h_m$,如图1所示,我们可以将每一层看作是一个马尔科夫链的状态:$h_i \to h_{i+1}$。根据DPI,我们有:
$$H(X) \geq I(X; h_1) \geq I(X; h_2) \geq \dots \geq I(X; h_m) \geq I(X; \hat{Y}) \
I(X; Y) \geq I(h_1; Y) \geq I(h_2; Y) \geq \dots \geq I(h_m; Y) \geq I(\hat{Y}; Y)$$
DNN的设计目的是学习如何描述$X$,以便预测$Y$;最终,将$X$压缩成只包含与$Y$相关的信息。Tishby将这一过程描述为“相关信息的逐次细化”。
信息平面定理
DNN依次实现了$X$的内部表示,一组隐藏层${T_i}$。根据信息平面定理,通过它的编码器和解码器信息来描述每一层,编码器即对输入数据$X$编码,而解码器则将当前层中的信息转换为目标输出$Y$。
准确地说,在一个信息平面图中:
- X轴:样本$T_i$复杂度由编码器互信息$I(X;T_i)$决定,样本复杂度是指你需要多少个样本来达到一定的准确性和泛化。
- Y轴:精度(泛化误差),由解码器互信息$I(T_i;Y)$决定。
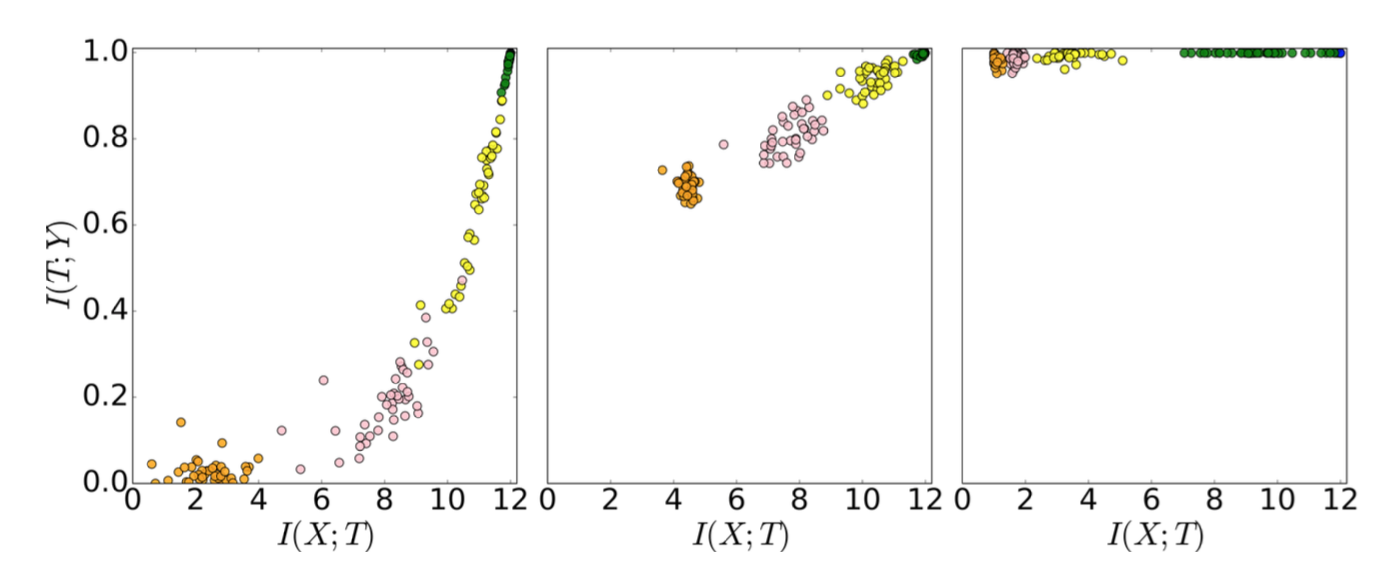
图2:50个DNN隐藏层的编码器和解码器的交互信息。不同层有不同色彩的编码器,绿色是紧挨着输入的一层,橙色是离输入最远的一层。有三个快照,分别是初始阶段、400个阶段和9000个阶段。
图2中的每个点表示一个隐含层的编码器或解码器的互信息(不采用正则化;没有权重衰减,没有丢失,等等)。它们按照预期的那样向上移动,因为关于真实标签的知识在增加(准确性在提高)。在早期阶段,隐藏层了解了很多关于输入$X$的信息,但是之后它们开始压缩以忘记输入的一些信息。Tishby认为,“学习的最重要的部分实际上是遗忘”。
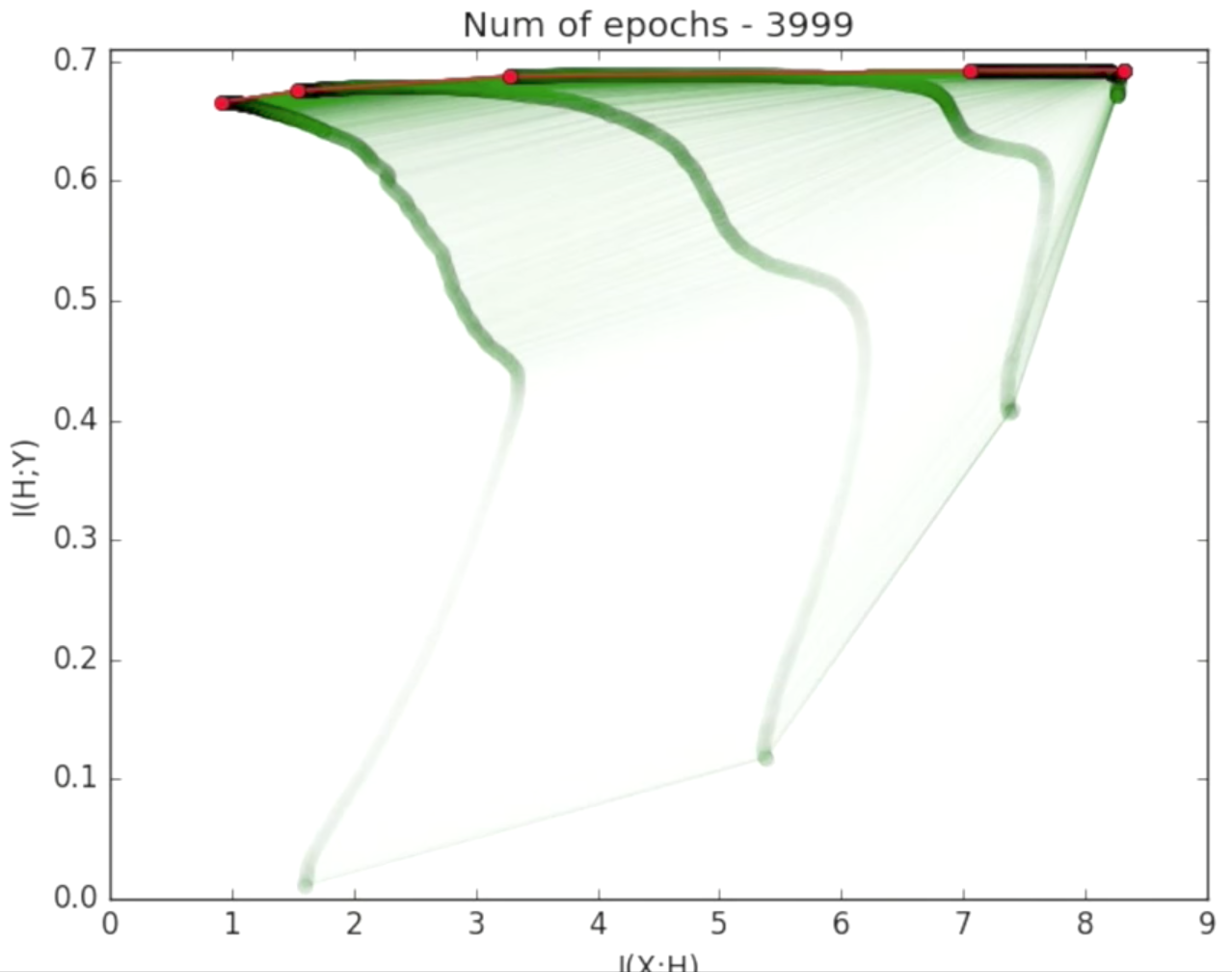
图3:这是图2的汇总视图。在泛化误差变得非常小之后进行了压缩。
两个优化阶段
对各层权重的均值和标准差的及时跟踪还显示了训练过程的两个优化阶段。
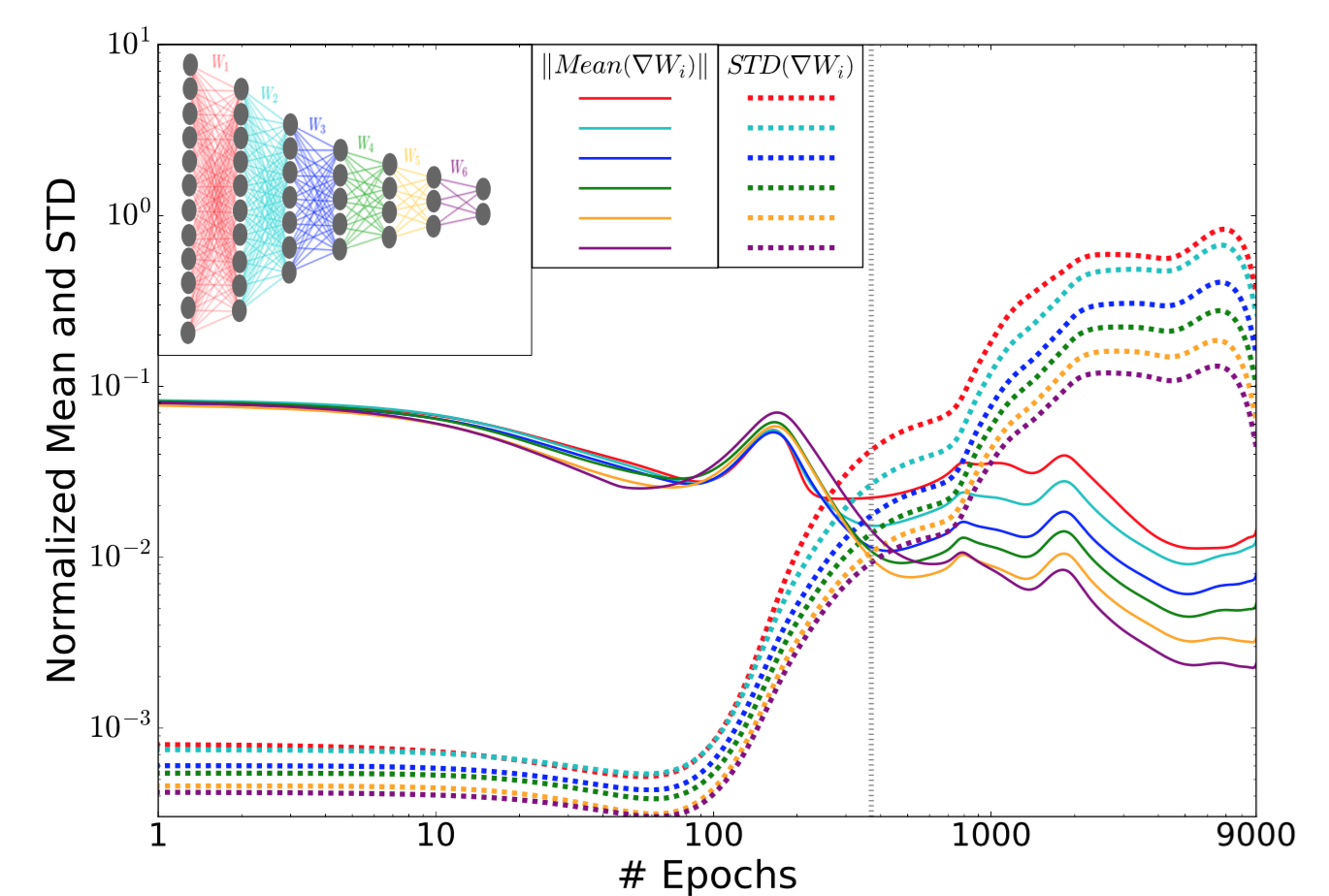
图4:各层权重梯度的均值和标准差的范数作为训练函数。不同的层用不同的颜色。
在早期阶段中,平均值比标准差大三个量级。 经过足够的时间段后,误差趋于饱和,随后标准差变得更大。离输出越远的层,噪声就越大,这是因为噪声可以通过反向传播过程放大和累积(而不是由于层的宽度)。
学习理论
“旧的”泛化
经典学习理论定义的泛化范围为:
$$\epsilon^2 < \frac{\log|H_\epsilon| + \log{1/\delta}}{2m}$$
- $\epsilon$:训练误差与泛化误差的差值。泛化误差衡量的是一个算法对前所未见的数据的预测有多准确。
- $H_\epsilon$: 假设,通常我们假设大小为$\vert H_\epsilon \vert \sim (1/\epsilon)^d$.
- $\delta$: 信度。
- $m$: 训练样本的数目。
- $d$:假设的VC维度。
该定义指出,训练误差和泛化误差之间的差异受假设空间大小和数据集大小的限制。假设空间越大,泛化误差就越大。
但是,它不适用于深度学习。网络越大,需要学习的参数越多。有了这种泛化界限,较大的网络(较大的$d$)会有更糟的界限。我们直觉上会认为更大的网络能够实现更好的性能和更高的表达能力。这里却是和直觉相反。
“新的”输入压缩
为了应对这种违反直觉的观察数据,Tishby等人提出了DNN的新输入压缩范围。
首先让我们将$T_\epsilon$作为输入变量$X$的$\epsilon$分区。此分区将有关标签同质性的输入压缩为小单元格,所有单元格可以覆盖整个输入空间。如果预测输出二进制值,则可以用$2^{\vert T_\epsilon \vert}$代替假设的基数$\vert H_\epsilon \vert$。
$$|H_\epsilon| \sim 2^{|X|} \to 2^{|T_\epsilon|}$$
当$X$比较大时,$X$的大小大约是$2^{H(X)}$。ϵ所在的每个单元格的大小是$2^{H(X \vert T_\epsilon)}$。因此,我们有$\vert T_\epsilon \vert \sim \frac{2^{H(X)}}{2^{H(X \vert T_\epsilon)}} = 2^{I(T_\epsilon; X)}$。那么,输入压缩范围就成了:
$$\epsilon^2 < \frac{2^{I(T_\epsilon; X)} + \log{1/\delta}}{2m}$$
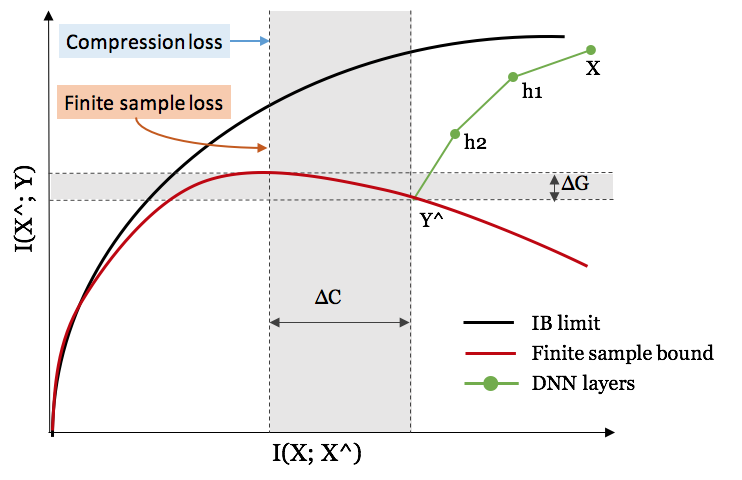
图5:黑线是可实现的最佳IB极限。在一个有限的样本集上训练时,红线对应样本外IB失真的上限。ΔC是复杂性的差距和ΔG是泛化的差距。
网络和训练数据的大小
更多隐藏层的好处
拥有更多的层会给我们带来计算上的好处,并加快训练过程,以获得更好的泛化效果。
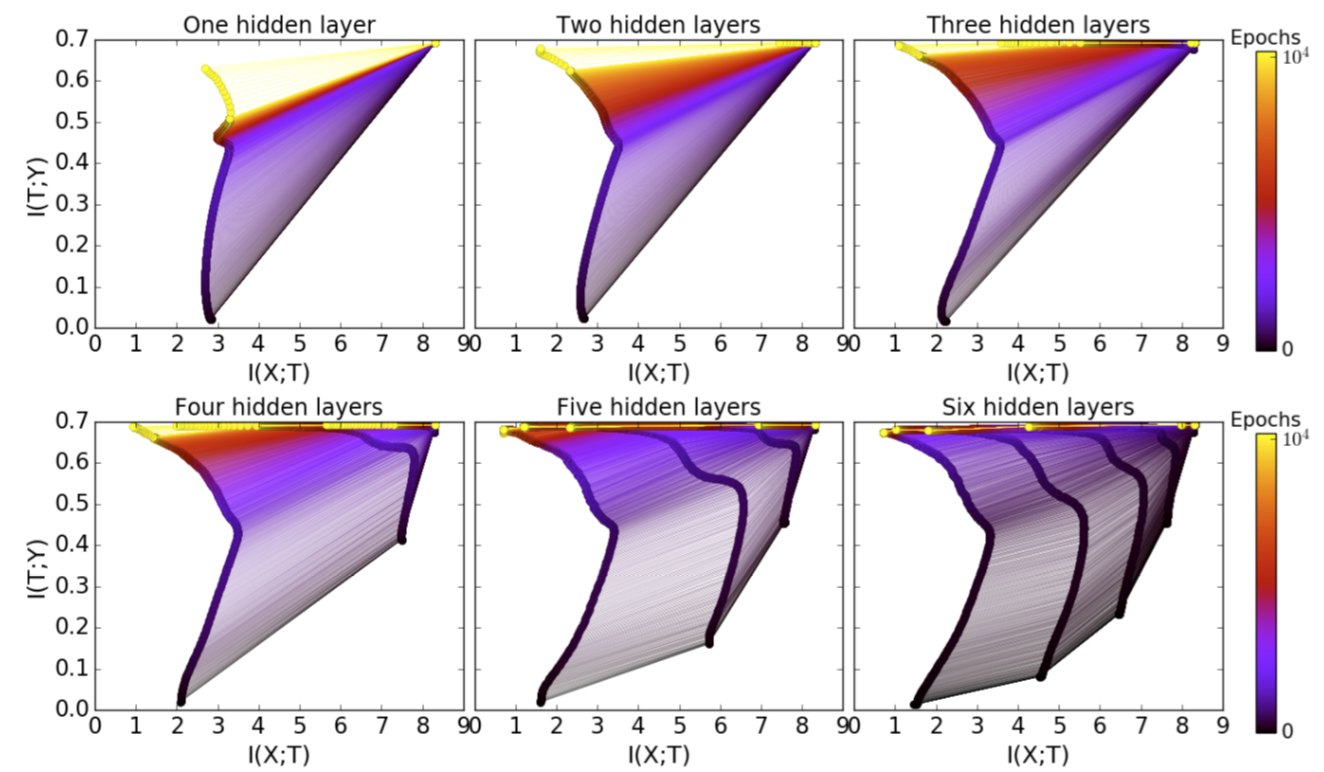
图6:有更多的隐藏层,优化时间更短(阶段更少)。
通过随机松弛算法进行压缩:根据扩散方程,k层的松弛时间与该层压缩量$\Delta S_k$: $\Delta t_k \sim \exp(\Delta S_k)$的指数成正比。我们可以按照$\Delta S_k = I(X; T_k) - I(X; T_{k-1})$计算层压缩。因为$\exp(\sum_k \Delta S_k) \geq \sum_k \exp(\Delta S_k)$,所以我们期望使用更多的隐藏层(更大的$k$)来使训练周期呈指数式减少。
更多训练样本的好处
拟合更多的训练数据需要通过隐藏层捕获更多的信息,随着训练数据量的增加,解码器互信息$I(T;Y)$ (还记得吗,这与泛化误差直接相关)被推高,更接近理论IB的边界。Tishby强调,与标准理论不同,决定泛化的是互信息,而不是层的大小或VC维度
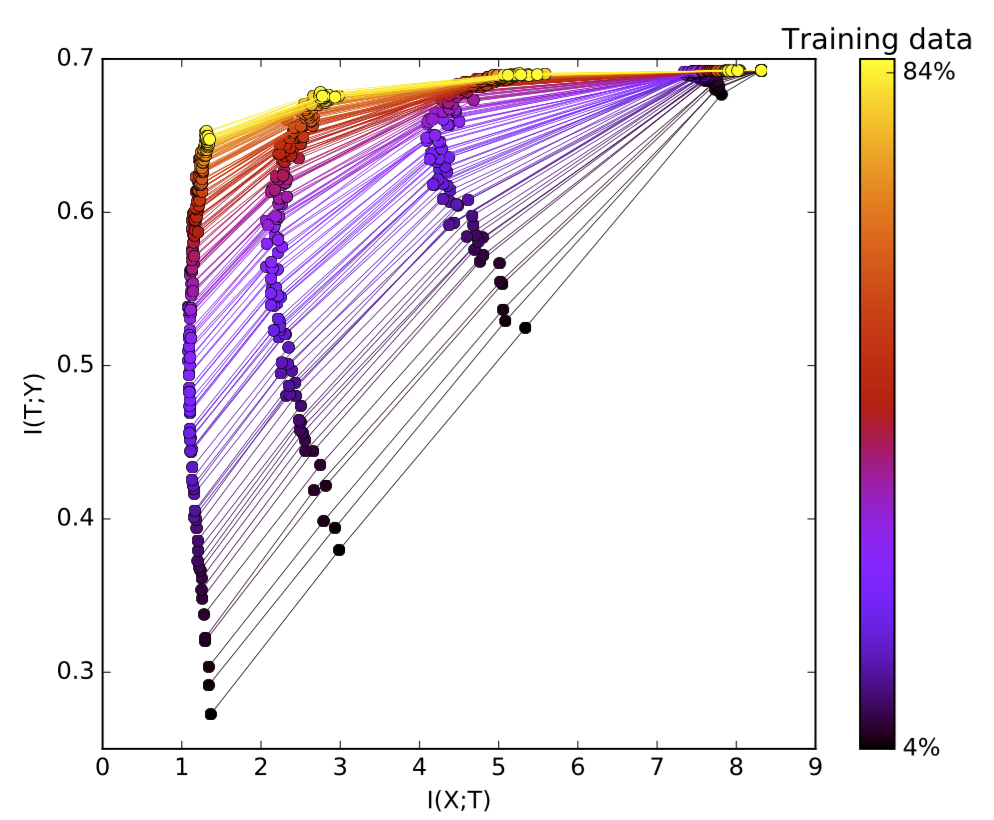
图7:不同大小的训练数据用不同颜色编码。这里绘制了多个聚合网络的信息平面。训练数据越多,泛化效果越好。
原文链接:https://lilianweng.github.io/lil-log/2017/09/28/anatomize-deep-learning-with-information-theory.html
搜索技术问答的公众号:老齐教室
在公众号中回复:老齐,可查看所有文章、书籍、课程。
觉得好看,就点赞转发
若你觉得我的文章对你有帮助,欢迎点击上方按钮对我打赏

关注微信公众号,读文章、听课程,提升技能
