“线性回归模型正则化”笔记
2020-04-18
损失函数与风险
机器学习模型建立在以“误差”最小化为目的的基础上的:
- 将模型应用到测试集中,测试结果与实际情况的误差是我们通常认为的“误差”,这种误差我们通常称做一般误差,亦被称为期望风险。
- 以最小化模型在训练集中的“误差”为目的的算法中的那个“误差”,是经验误差,对应于期望风险,它又被称作经验风险。而用于表示经验风险(也可称经验损失)的函数:
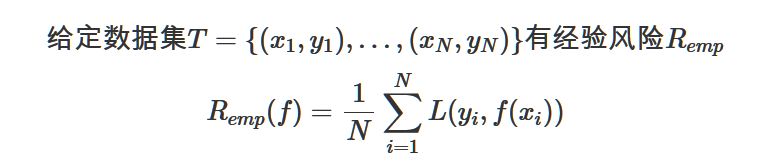
此处函数$L$有多重形式。如下所示:

下面的是成本函数。计算误差所用的成本函数,也称为损失函数。上面图中是常用的损失函数形式。

- 成本函数和损失函数确实没有什么区别。但我们在线性回归中用的J(θ)严格来讲仅仅是一个用于衡量经验误差大小的函数,它与现在我们所讨论的损失函数有一点点区别就是它可以为了方便计算而做出一些修改,也就是说只要它适合我们用于建立模型即可,而目的并不是严格计算出经验风险。
- 成本函数仅是为了方便计算而用于表示风险的一个计算式,经验风险函数$R_{emp}$则更偏向于严格衡量模型的经验风险。也正因此,极大似然估计也可以看作是经验风险最小化的一个策略。
一般来说,我们建立模型的基准都是通过最小化经验风险,但经验风险并不代表期望风险,也即测试集中的误差和训练集中的误差是有区别的,这就意味着,当经验风险真的最小化的时候,就会出现过拟合的现象,模型完美贴近训练集,但在测试集中往往会表现不佳。为了避免这一情况出现,也即防止过拟合出现,就有了结构风险最小化,而这个策略,事实上就等价于正则化。
正则化
正则化就是通过对模型参数进行调整(数量和大小),降低模型的复杂度,以达到可以避免过拟合的效果。正则化是机器学习中的一种叫法,其它领域内叫法各不相同:
机器学习把L1和L2叫正则化,统计学领域叫惩罚项,数学领域叫范数。
正则化是一个典型的用于选择模型的方法。它是结构风险最小化策略的实现,是在经验风险上加一个正则化项或惩罚项。正则化项一般是模型复杂度的单调递增函数,模型越复杂,正则化值就越大。
定义结构风险:
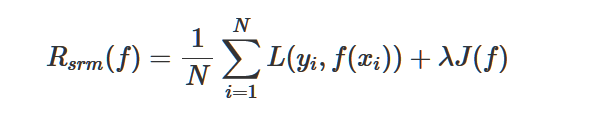
- 前面一项就是经验风险,即损失项,用于衡量模型与数据的拟合度
- 后一项中的
J(f)就表示模型的复杂度 ,它是定义在假设空间F上的泛函(通常是指一种定义域为函数,而值域为实数的“函数”。换句话说,就是从函数组成的一个向量空间到实数的一个映射。也就是说它的输入为函数,而输出为实数,来自维基百科),模型f越复杂,复杂度J(f)就越大;反之,模型越简单,复杂度J(f)就越小。也就是说,复杂度表示了对复杂模型的惩罚。λ≥0是系数,用以权衡经验风险和模型复杂度。结构风险小的模型往往对训练数据以及位置的测试数据都有较好的预测。 - λJ(f)称之为正则化项。
贝叶斯估计中的最大化后验概率估计就是结构风险最小化的一个例子。
- 当模型是条件概率分布、损失函数是对数损失函数、模型复杂度由模型的先验概率表示时,结构风险最小化就等价于最大化后验概率估计。
一般线性回归我们用均方误差作为损失函数。损失函数的代数法表示如下:

如果写成矩阵:
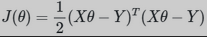
正则化项可以取不同的形式。例如,回归问题中,损失函数是平方损失,正则化项就可以是参数向量的L2范数/L1范数
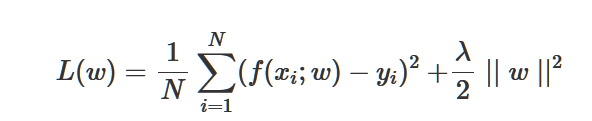
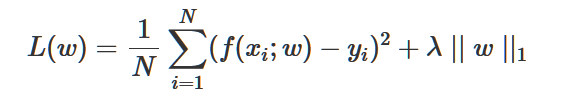
正则化的作用就是选择经验风险与模型复杂度同时较小的模型
L2范数优化简单,因为它假设参数服从了高斯分布,利于防止过拟合;
使用L2范数,其回归称为Ridge回归。在不抛弃任何一个特征的情况下,缩小了回归系数,使得模型相对而言比较的稳定,不至于过拟合。
对于这个损失函数,一般有梯度下降法和最小二乘法两种极小化损失函数的优化方法,而scikit中的Ridge类用的是最小二乘法。
RidgeCV类的损失函数和损失函数的优化方法完全与Ridge类相同,区别在于验证方法。
L1范数优化稍复杂一些(一个常用的方法是LASSO),它假设参数服从双指数分布,可以增强得到的问题的解的稀疏性。L1正则化通常称为Lasso回归
- Lasso回归可以使得一些特征的系数变小,甚至还是一些绝对值较小的系数直接变为0。增强模型的泛化能
- Lasso回归的损失函数优化方法常用的有两种,坐标轴下降法和最小角回归法。Lasso类采用的是坐标轴下降法
- sklearn中的Lasso类并没有用到交叉验证之类的验证方法
- LassoCV类的损失函数和损失函数的优化方法完全与Lasso类相同,区别在于验证方法。当我们面临在一堆高维特征中找出主要特征时,LassoCV类更是必选。当面对稀疏线性关系时,LassoCV也很好用。
- LassoLars类的损失函数和验证方法与Lasso类相同,区别在于损失函数的优化方法。LassoLars类采用的是最小角回归法
- LassoLarsCV类的损失函数和损失函数的优化方法完全与LassoLars类相同,区别在于验证方法,交叉验证。
从贝叶斯估计的角度来看,正则化项对应于模型的先验概率,可以假设复杂的模型有较小的先验概率,简单的模型有较大的先验概率。
ElasticNet(弹性网络)可以看做Lasso和Ridge的中庸化的产物。它也是对普通的线性回归做了正则化,但是它的损失函数既不全是L1的正则化,也不全是L2的正则化,而是用一个权重参数ρρ来平衡L1和L2正则化的比重
L2正则化:岭回归
通过最小二乘法推导出多元线性回归的求解公式
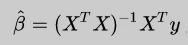
这个公式有一个问题:X不能为奇异矩阵,否则无法求解矩阵的逆。岭回归的提出恰好可以很好的解决这个问题,它的思路是:在原先的β的最小二乘估计中加一个小扰动λI,这样就可以保证矩阵的逆可以求解,使得问题稳定。公式如下:
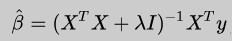
这个公式可以通过对结构化风险函数求偏导推出来
过拟合
评判模型好坏的标准是:不但对于训练的数据集有很好的拟合效果,而且对于未知的新的数据(测试集)也同样拥有好的效果,即拥有好的泛化能力。
如果过分地的学习就会导致模型缺少泛化能力,即过拟合。
常见的避免过拟合方法:
- 增加数据量
- 简化模型
- 交叉验证
- 正则化
参考资料:
若你觉得我的文章对你有帮助,欢迎点击上方按钮对我打赏

关注微信公众号,读文章、听课程,提升技能
