什么是量子计算

2020-05-26

作者：Jonathan Hui

翻译：老齐

量子位是量子计算中的核心单位，借助于叠加态，我们可以将量子位编码成指数级的信息，这些信息可以比传统的计算机产生的信息多得多。在本文中，首先要介绍一下量子计算的基本原理，以及量子力学中的一些法则。

叠加态

叠加态是一个重要的概念，因为这要牵扯到量子位。还是从自旋的数学模型开始吧，别害怕！它很简单。在这里我们会放慢学习的节奏，从而你能够有时间熟悉量子力学中的一些符号，这些符号构成了量子力学中那些优美的函数。另外，我们这里用到的数学，远比你想象得简单。

当我们说一个叠加态中的粒子的自旋时，其含义非常简单，就是指自旋向上（up spin）和自旋向下（down spin）的线性组合，用狄拉克符号表示就是这样的：

前面的系数 $\alpha$ 叫做振幅（amplitude）

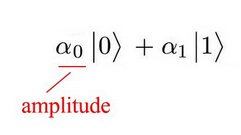
此处的自旋向上和自旋向下就相当于向量的基，类似于直角坐标系中x、y两个向量的基那样，其写法也类似。

用狄拉克符号表示，$|\Psi \rangle$ 表示量子态（quantum state），它其实是矩阵。上图中的 superposition 所标示的，就是自旋的线性组合，它就是一种叠加态，也就是一种量子态。

$|0\rangle$ 和 $|1 \rangle$ 是两个正交向量，可以写成：

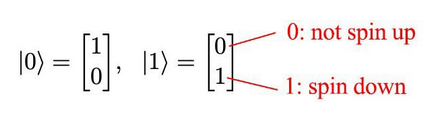
或者是：

$$\langle0| = \begin{bmatrix}1\0\end{bmatrix}，\langle 1|=\begin{bmatrix}0\1\end{bmatrix}$$

线性代数，没那么复杂。在这里，我们只是用狄拉克符号将线性代数中的写法简化了。一旦你熟悉了，我们可以用很多简单的方式进行表示。例如，两个正交向量的内积，用 $\langle0|1\rangle$ 表示，它们的结果总是 $0$。而任何两个叠加态的内积则为 $1$。

$$\langle0|1\rangle = 0，\langle 1|1 \rangle = \langle \Psi|\Psi \rangle=1$$

下面所示的是更复杂一些的叠加态以及对应的矩阵表示。

$$|+\rangle=\frac{|0\rangle+|1\rangle}{\sqrt {2}}=\frac{1}{\sqrt{2}}\begin{bmatrix}1\1\end{bmatrix}$$
$$|-\rangle=\frac{|0\rangle-|1\rangle}{\sqrt {2}}=\frac{1}{\sqrt{2}}\begin{bmatrix}1\-1\end{bmatrix}$$

通过对自旋向上和自旋向下的测量，我们能够控制叠加态，但是，当我们测量了自旋向上，叠加态可能坍缩为某一种状态，$|0 \rangle$ 或 $|1 \rangle$。这是量子力学的核心思想，也是自然的运作规律。

假设一个粒子状态表示为：

$$\frac{1}{\sqrt{2}}|0\rangle + \frac{1}{\sqrt{2}}|1\rangle$$

它坍缩为另外一种状态的概率是相应振幅的平方，事实表明，这个模型与实验结果相符的非常好，因此，测量粒子的自旋向上的概率是 $\frac{1}{2}$。

这是我们必须要掌握的基本原则，所有状态的测量概率之和是 $1$ （即 $\langle \Psi | \Psi \rangle=1$），计算方式如下：

$$|\alpha_0|^2+|\alpha_1|^2$$

我们可以把叠加态想象成一个单位球体表面的一个点，自旋向上和自旋向下恰恰是这个球体的北极和南极，那么图中的红点就表示了另外一种叠加态，测量它的时候，自然迫使它选择一边，向上还是向下。

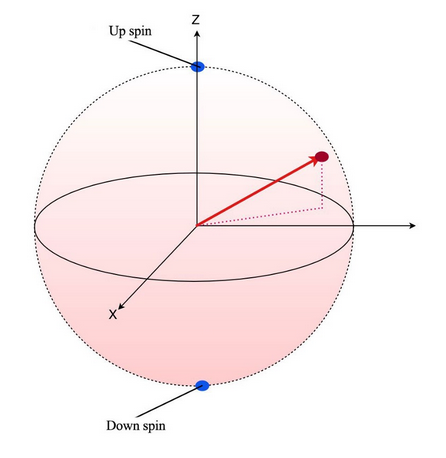
但是，上面图示也不是非常准确。为了更贴近真实的直观表示，像上图那样的球体称为布拉赫球，其中的振幅 $\alpha$ 也可以是复数，例如：

$$\frac{1-i}{2\sqrt{2}}|0\rangle+\frac{1+i}{2\sqrt{2}}|1\rangle$$

这样，叠加态的值有6种可能。

通过计算振幅的范数，就得到了概率，方法就是振幅与其共轭相乘，例如 $3+4i$ 的共轭是 $3-4i$，表示为：

$$\alpha_i^* \alpha_i$$

下面，我们简要比较一下比特（bit）和量子位。一个比特表示两个可能数值中的一个，不是 $0$ 就是 $1$。一个量子位表示单位球面上的点。在第一个回合中，量子位在表示的状态数量上更胜一筹。

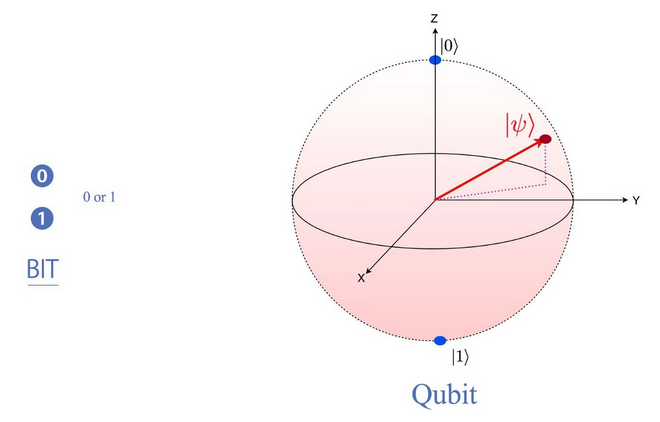
另外，我们可以通过量子态的组合而成一个复杂系统，根据量子力学的原理，一个复杂系统可以用张量积表示：

$$|v\rangle \otimes|w\rangle \quad or \quad |vw\rangle$$

其中

$$|a\rangle|b\rangle=|a\rangle \otimes |b\rangle = \begin{bmatrix}xu\xv\\vdots\yu\yv\\vdots\end{bmatrix}$$

例如，这个复杂系统中包括2个自旋向下和1个自旋向上：

$$\begin{equation}\begin{split}|101\rangle &=|1\rangle \otimes |0\rangle \otimes |1\rangle \ &=\begin{bmatrix}0\1\end{bmatrix} \otimes \begin{bmatrix}1\0\end{bmatrix} \otimes \begin{bmatrix}0\1\end{bmatrix}\&= \begin{bmatrix}0&0&0&0&0&1&0&0\end{bmatrix}^T\end{split}\end{equation}$$

很快，我们就会看到，这是多么强大的系统，传统的计算是无法达到的，下面是一个3个量子位的示例：

$$\begin{equation}\begin{split}\frac{1}{\sqrt{2}}(|0\rangle +|1\rangle) \otimes |1\rangle \otimes |1\rangle &\equiv \frac{1}{\sqrt{2}}(|011\rangle+|111\rangle) \ &\equiv \frac{1}{\sqrt{2}}(|3\rangle + |7\rangle)\end{split}\end{equation}$$

下面的方程描述了2个量子位的系统，它由两个粒子的自旋组成。

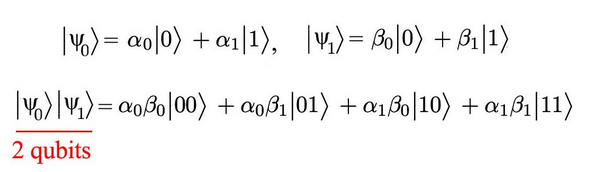
因此，新的量子态有4个基向量，分别是$|00\rangle、|01\rangle、|10\rangle、|11\rangle$，相应的是4个复数的系数。

$$|\mathbb \alpha\rangle=\alpha_{00}|00\rangle+\alpha_{01}|01\rangle+\alpha_{10}|10\rangle+\alpha_{11}|11\rangle$$

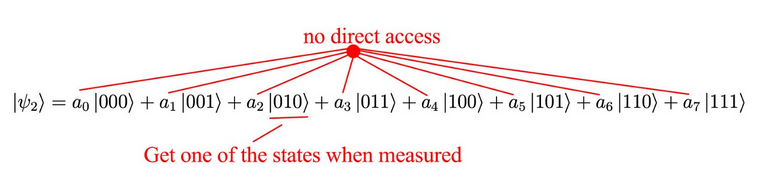
如果是3量子位，就是8个基向量了：

$$|\psi_2\rangle=\alpha_{0}|000\rangle+\alpha_{1}|001\rangle+\alpha_{2}|010\rangle+\alpha_{3}|011\rangle+\alpha_{4}|100\rangle\alpha_{5}|101\rangle\alpha_{6}|110\rangle+\alpha_{7}|111\rangle$$

按照这样的组合，64量子位，则有：