在上一篇中，使用for循环绘制了正多边形。本篇要在此基础上，进一步优化上一篇的程序。

从数学的角度来讲，正多边形（或者说正 $n$ 边形，$n \ge 3$）的外角和是 $360°$，那么每个外角的度数就是 $\frac{360°}{n}$，其中 $n$ 为多边形的边。根据上一篇所获得的经验，这个外角的度数，正好是小海龟在任何一点向右转的度数。

有了以上的数学认识，我们就可以轻松绘制任意正多边形了。

为了能让我们的程序更“智能”一些，先了解一个Python的内置函数：input()，这个函数式用来获得用户通过键盘输入的字符。打开IDLE，会首先看到下面图所示状态：

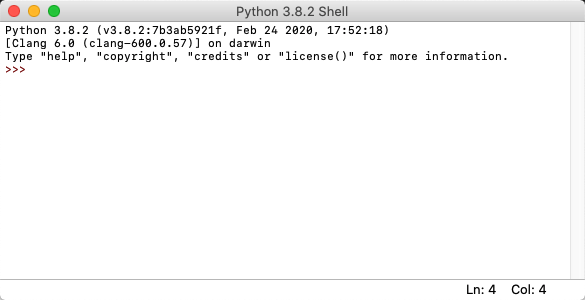
这种状态，我们称之为交互模式，也就是允许我们在提示符后面输入一行代码，然后敲回车，计算机（其实是Python解析器）就会执行这行代码。例如：

1
2

>>> 3 + 4
7

在交互模式中，输入 3+4 之后，敲回车，就返回了这条语句的计算结果。类似地，如果执行 input()函数，会是这样：

在input()函数里面的文字，是提示语（绿色文字），也可以不写。注意，提示语的外围，是用英文状态下的引号包裹，必须是英文状态下的引号——英文的引号，可以是单引号，也可以是双引号，在引号包括下的东西称为字符串。

执行了上面的函数之后，就出现了下面一行的提示语（蓝色文字），然后就是光标，等待用户通过键盘输入内容。例如按下键盘上的数字7，然后敲回车键，得到下图显示的效果：

这说明input()函数已经捕获了我们通过键盘输入的数字，并且返回了'7'，这是一个字符串——符合前面提到的字符串的特点，用引号包裹。

为了进一步理解input()的作用，再执行下面的代码：

1
2
3
4
5
6
7
8
9

>>> a = input('please input a number:')
please input a number:4
>>> a
'4'
>>> a + 3
Traceback (most recent call last):
  File "<pyshell#4>", line 1, in <module>
    a + 3
TypeError: can only concatenate str (not "int") to str

第1行中，a = input('please input a number:')的含义是，将捕获的键盘输入字符，用变量a引用，在第3行，就显示了a这边变量引用的内容，是通过键盘输入的数字4，但是，注意，它是一个字符串。

执行第5行，报错了。注意阅读报错信息——一定要有耐心阅读报错信息，can only concatenate str (not "int") to str的意思是不能将字符串和整数连接起来。在a + 3中，变量a引用的对象是字符串，而3是一个整数，这两个是不能相加的。在Python中，必须是同种类型的才能相加——不仅仅是相加，其他运算也是如此。怎么办？可以进行类型转化。下面演示的就是把字符串转化为整数的方法。

1
2

>>> int(a) + 3
7

int(a)就是把字符串转变为了整数，然后就能跟整数3相加了。

打开前面使用过的文件myturtle.py，对其中代码做如下修改：

1
2
3
4
5
6
7
8
9

from turtle import *

shape("turtle")
n = input("请输入多边形的边数：")
n = int(n)
alpha = 360 / n
for i in range(n):
    forward(100)
    right(alpha)

这段代码中，第4行使用了刚刚学习的input()函数，目的就是用户可以通过键盘，输入想要绘制的多边形的边数。注意第5行，根据前面讲过的，要将在第4行获得的键盘输入的数字转化为整数，然后第6行才能做除法，这样就得到了该正n边形的外角的度数，将它用于第9行，作为right()的参数。

另外，第7行，range()内的参数，也要修改，n边形，就要循环n次。

保存文件，执行。注意观察显示的界面，那只小海龟趴着不动，为什么？再观察交互模式，其实是等着用户输入边数呢。

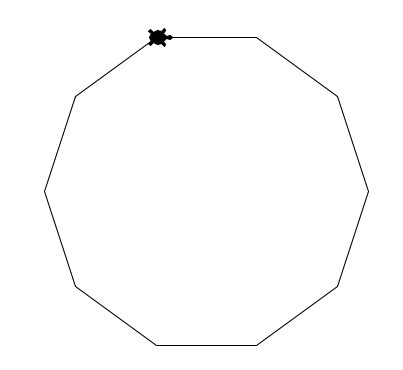
比如输入：10，然后回车。就会看到小海龟按照程序中指定的方式画图了，一个正10边形跃然“屏”上。

在上面的程序中，我们实现了正多边形边数的键盘输入，那么，正多边形的边长能不能通过键盘输入呢？读者可以思考一下，然后尝试。下面的代码供参考。

1
2
3
4
5
6
7
8
9
10
11

from turtle import *

shape("turtle")
n = input("请输入多边形的边数：")
length = input("请输入多边形的边长：")
n = int(n)
length = int(length)
alpha = 360 / n
for i in range(n):
    forward(length)
    right(alpha)

我执行这个程序，分别输入了下图所示的两个值：

我让小海龟画一个正100边的图形，结果什么样？

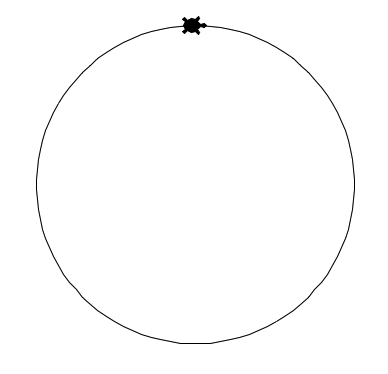
怎么看起来像圆？不过仔细观察，会发现，没有圆那么圆滑，不是圆，是多边形。

“看起来像圆”，这说明当多边形的边数很多的时候，这个多边形就接近圆了。在数学上，人们很早就研究了正多边形和它的外接圆的关系，也发现了这样的规律，当多边形的边数阅读，该多边形与外接圆越接近——这是一种近似地计算圆的周长的方法。中国古代，把这称之为“割圆术”，魏晋时期数学家刘徽于公元263年撰写的《九章算术注》有详细的记载。对此有兴趣深入了解的同学，可以查阅有关资料。

在本篇中，主要学习使用input()函数，实现了通过键盘输入数字，绘制任意边长和边数的多边形，并在最后实现了“割圆术”。读者不妨发挥自己的想象力，修改程序，看看还有什么新发现？

专注于软件和AI的公众号

老齐教室