b01.01 函数

从初中代数，就已经引入了函数这个概念，其英文单词是function，中文翻译为函数，这个词语是由大清朝数学家李善兰所翻译，他在所著的《代数学》书中解释：“凡此变数中函（包含）彼变数者，则此为彼之函数”（台湾省的有关资料中，常将变量称为“变数”）。

函数这个数学名词是莱布尼兹在1694年开始使用的，当时他用这个名词描述与曲线相关的量，如曲线的斜率等。现在，我们将莱布尼兹所说的函数称为函数的导数。此后，很多数学家对函数做了深入研究，并且给出了不同的定义，例如：

• 1718年，约翰·伯努利把函数定义为“一个变量的函数是指由这个变量和常量以任何一种方式组成的一种量。”
• 1748年，伯努利的学生欧拉在《无穷分析引论》一书中说：“一个变量的函数是由该变量和一些数或常量以任何一种方式构成的解析表达式”，例如 $f(x)=\sin(x)+x^{2}$ 。
• 1775年，欧拉在《微分学原理》一书中又提出了函数的一个定义：“如果某些量以如下方式依赖于另一些量，即当后者变化时，前者本身也发生变化，则称前一些量是后一些量的函数。”
• 到19世纪末，数学家开始尝试利用集合论来进行数学的形式化。他们试图将每一个数学对象都定义为集合。狄利克雷给出了现代正式的函数定义。

函数及其图像

函数是一种用以描述世界的工具。一个函数，可以用表达式、图像、表格或者语言进行描述。

函数及其定义域和值域

定义 函数是从一个集合 $\mathbb{D}$ 到另一个集合 $\mathbb{Y}$ 间的对应法则，通常记作记作 $f:\mathbb{X}\to\mathbb{Y}$ ，其中 $f$ 表示对应法则。

更一般的写法：

$$y=f(x)$$

符号 $f$ 表示函数；$x$ 叫做自变量（independent variable），是函数 $f$ 的输入；$y$ 是因变量（dependent variable），是函数 $f$ 关于 $x$ 的输出。如下图所示。

显然，$x\in\mathbb{D}$ ，集合 $\mathbb{D}$ 中所有可以作为自变量的元素构成了函数的定义域（domain）；$f(x)$ 的所有输出所构成的集合称为值域（range），值域则必然是集合 $\mathbb{Y}$ 中的元素，即 $y\in\mathbb{Y}$ 。

例如函数 $y=\sqrt{x}$ 的定义域是 $[0,\infty)$ ，值域是 $[0,\infty)$ 。

函数图像

除了用表达式表示函数之外，还会用图像表示函数。以二维的为例，函数的每个自变量与因变量可以构成笛卡尔直角坐标系中的一个点。

$${(x,f(x)|x\in\mathbb{D}}$$

按照上式，将所有点连成线，即为函数图像。例如函数 $y=x^2$ 的图像：

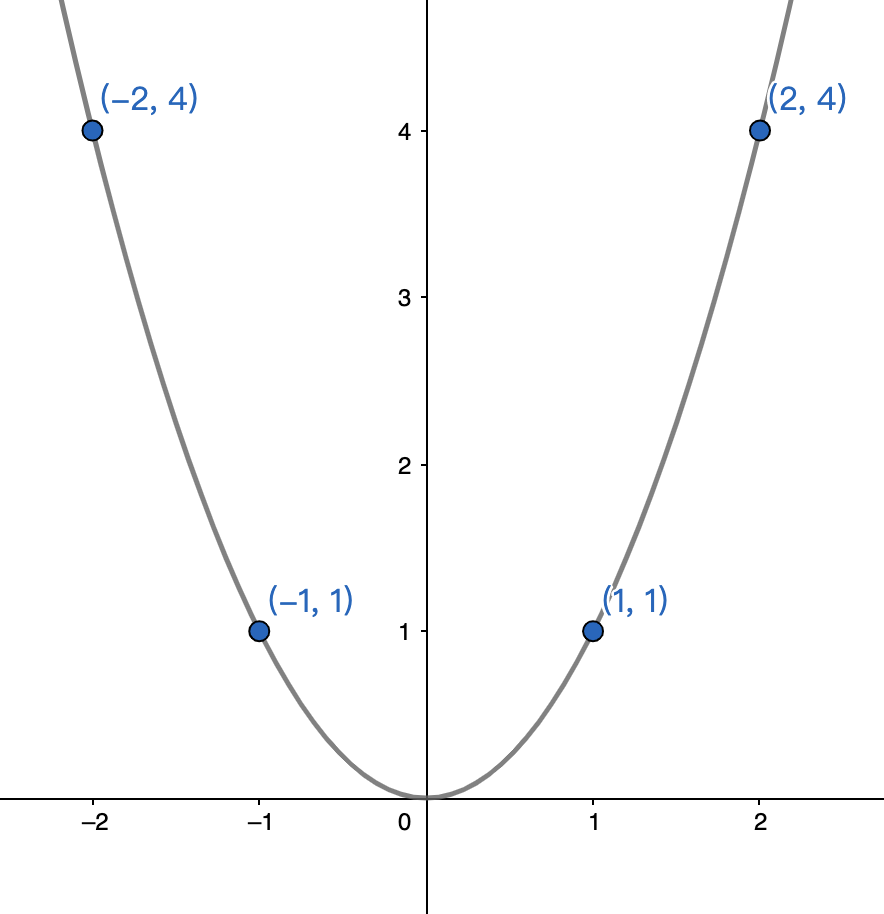
分段函数

有时一个函数别划分为几部分，各个部分的函数形式不同，例如：

$$f(x)=\begin{cases}-x,\quad&{x\lt{0}}\x^2,\quad&{0\le{x}\le{1}}\1,\quad&{x\gt{1}}\end{cases}$$

增函数和减函数

定义 令区间 $\mathbb{I}$ 上的函数为 $f$ ，$x_1$ 和 $x_2$ 是这个区间上两个不同的点，且 $x_1\lt{x_2}$ ：

• 如果 $f(x_1)\gt{f(x_2)}$ ，则函数 $f$ 称为区间 $\mathbb{I}$ 上的减函数（decreasing function）
• 如果 $f(x_1)\lt{f(x_2)}$ ，则函数 $f$ 称为区间 $\mathbb{I}$ 上的增函数（increasing function）

函数的奇偶性

定义 设函数 $y=f(x)$ ，$x$ 在函数定义域内：

• 若 $f(-x)=f(x)$ ，则函数 $f$ 是偶函数（even function）
• 若 $f(-x)=-f(x)$ ，则函数 $f$ 是奇函数（odd function）

例如：函数 $f(x)=x^2+1$ ，$f(-x)=(-x)^2+1=x^2+1=f(x)$ ，故为偶函数。如果将 $y=x^2$ 与 $y=x^2+1$ 相比较，如下图所示，即是 $y=x^2$ 沿 $y$ 轴向上移动一个单位得到了 $y=x^2+1$ 。

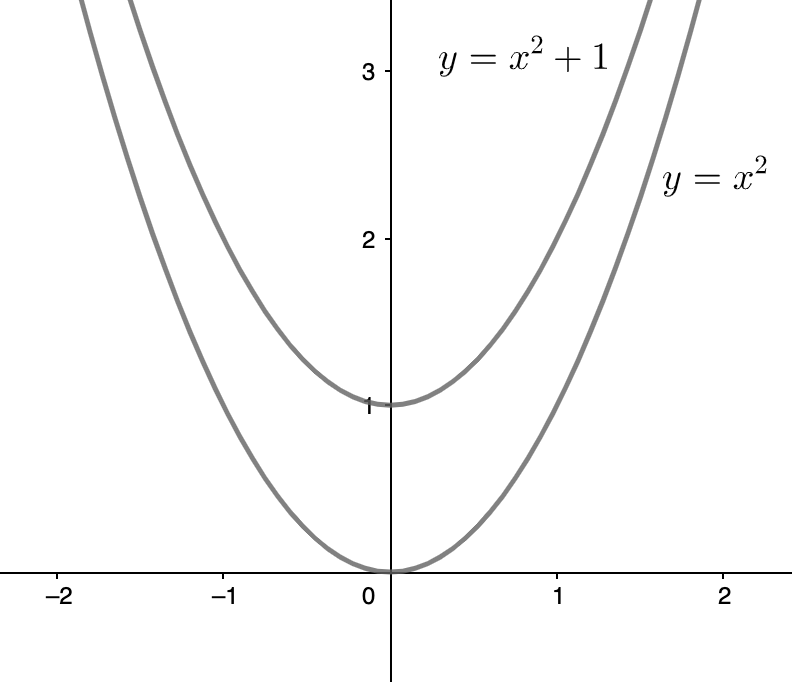
并且，从图像中可以看出来，偶函数是关于 $y$ 轴对称的函数，这个结论可以推广到所有的偶函数中。

再如：函数 $f(x)=x$ ，显然是一个奇函数，如下图所示，奇函数的特点是关于坐标原点对称。但是，函数 $f(x)=x+1$ ，虽然也可以看做是函数 $f(x)=x$ 向上移动一个单位，但 $f(-x) = -x+1\ne-(x+1)=-f(x)$ ，故它不是奇函数，也不是偶函数——由此可知，函数并非是奇函数和偶函数的并集——“不是奇函数，就是偶函数”，这句话是错误的。

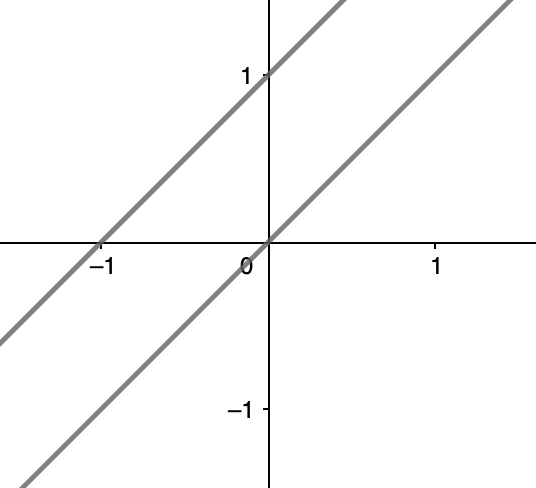
常见函数

1. 线性函数：$f(x)=mx+b$ （注意，要区分此处的“线性函数”和“线性空间”，具体请参阅《机器学习数学基础》一书中的详细内容）。

2. 反比例函数：$f(x)=\frac{1}{x}$

3. 指数函数：$f(x)=x^a$ ，其中 $a$ 是常数。

   1. $f(x)=x^n$ ，$n$ 是正整数，下图分别表示了 $n=1,2,3,4,5$ 的函数图像。

      指数是正整数的指数函数比较

   2. $f(x)=x^a$ ，$a=-1$ 或 $a=-2$

      当 $a=-1$ 时，即 $f(x)=x^{-1}=\frac{1}{x}$ ，是反比例函数，其图像如下。此函数等效于 $xy=1$ ，注意 $x\ne{0}$ 。并且是奇函数。

      反比例函数

      当 $a=-2$ 时，即 $f(x)=x^{-2}=\frac{1}{x^2}$ ，且为偶函数。其图像如下所示：

      a=-2 时的函数图像

   3. $a=\frac{1}{2},\frac{1}{3},\frac{3}{2},\frac{2}{3}$

      这几种结果，分别对应常用的函数，其图像如下所示：

      几种常见指数函数比较

4. 多项式：$p(x)=a_nx^n+a_{n-1}x^{n-1}+\cdots+a_1x+a_0$ ，其中 $n$ 为非负整数，$a_0,a_1,\cdots,a_n$ 是实数，称为多项式的系数。多项式的定义域为 $(-\infty,\infty)$ 。若系数 $a_n$ 不为零，则 $n$ 称为多项式的次或阶。前面所说的线性函数 $f(x)=mx+b$ ，若 $x\ne{0}$ ，则为 $1$ 次多项式；如果多项式的次数（阶数）是 $2$ ，即为二次函数，常表示为 $p(x)=ax^2+bx+c$ 。

5. 有理函数：$f(x)=\frac{p(x)}{q(x)}$ ，其中 $p$ 和 $q$ 分别是多项式，$q(x)\ne{0}$ 。例如：

   

   一个有理函数

6. 代数函数：对多项式利用代数运算符（加减乘除和幂运算）进行组合。所有的有理函数都是代数函数，但代数函数的范畴比有理函数更大。例如下图所示就是代数函数 $y=x^{\frac{1}{3}}(x-4)$ 的图像。

   代数函数图像

7. 三角函数：例如 $y=\sin(x)$ ，后续内容会专门介绍常用的6个三角函数。

8. 幂函数：$f(x)=a^x$ ，其中 $a\gt{0}$ 且 $a\ne{1}$ ，称作底。定义域 $(-\infty,\infty)$ ，值域 $(0,\infty)$ 。后续会专门探讨幂函数。

9. 对数函数：$f(x)=\log_ax$ ，其中 $a\ne{1}$ 是正数，它的反函数是幂函数。在后续内容中会专门对此进行探讨。

10. 超越函数：其形式不是代数的，包括三角函数、反三角函数等。例如悬线就是一种超越函数。后续内容中也会专门对此进行研究。