利用飞桨实现数字识别

2020-01-11

作者：燕清

数字识别，是机器学习和深度学习的经典案例。为此，此时用飞桨深度学习平台，也实现此案例。在本例中所用的数据集来自MNIST。

图1.MNIST图片示例

本文中，我们从简单的Softmax回归模型开始，带大家了解手写字符识别，并向大家介绍如何改进模型，利用多层感知机（MLP）和卷积神经网络（CNN）优化识别效果。

提示： 本文代码已经发布到在线实验平台，请关注本文微信公众号（扫描文末二维码），并回复：姓名+手机号+‘案例’，即可获得。

概述

首先，理解本文所使用的如下定义：

X，代表输入：MNIST图片是28×28 的二维图像，为了进行计算，我们将其转化为784维向量，即X=($x_0,x_1,…,x_{783}$)。
Y，代表分类器预测的输出：分类器的输出是10类数字（0-9），即Y=($y_0,y_1,…,y_9$)，每一维$y_i$代表图片分类为第i类数字的概率。
Labe，代表数字图片的真实标签：Label=($l_0,l_1,…,l_9$)，也是10维，但只有一个特征为1，其他都为0，即用稀疏矩阵表示数字。例如某张图片上的数字为2，则它对应的样本为(0,0,1,0,…,0)

Softmax回归(Softmax Regression)

最简单的Softmax回归模型是先将输入层经过一个全连接层得到特征，然后直接通过softmax函数计算多个类别的概率并输出。

X传到输出层，在激活操作之前，会乘以相应的权重 W ，并加上偏置变量 b ，如下式所示：

$$y_i = softmax(\sum_jW_{i,j}x_j + b_i)$$

其中

$$softmax(x_i) = \frac{e^{x_i}}{\sum_je^{x_j}}$$

对于有 N 个类别的多分类问题，指定 N 个输出节点，N 维向量经过softmax将区间化为 N 个[0,1]范围内的实数值，分别表示该样本属于这 N 个类别的概率。此处的 $y_i$ 即对应该图片为数字 i 的预测概率。

在分类问题中，我们一般采用交叉熵损失函数（cross entropy loss），公式如下：

$$L_{cross-entropy}(label, y) = -\sum_i label_i log(y_i)$$

多层感知机(Multilayer Perceptron, MLP)

Softmax回归模型采用了最简单的两层神经网络，即只有输入层和输出层，因此其拟合能力有限。为了达到更好的识别效果，我们考虑在输入层和输出层中间加上若干个隐藏层。

经过第一个隐藏层，可以得到 $H_1=ϕ(W_1X+b_1)$，其中ϕ代表激活函数，常见的有sigmoid、tanh或ReLU等函数。
经过第二个隐藏层，可以得到 $H_2=ϕ(W_2H_1+b_2)$。
最后，再经过输出层，得到的$Y=softmax(W_3H_2+b_3)$，即为最后的分类结果。

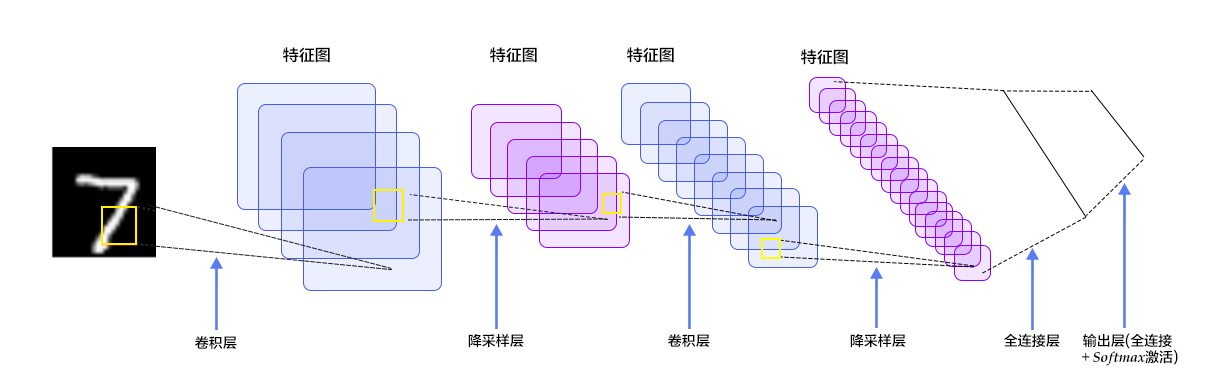
卷积神经网络(Convolutional Neural Network, CNN)

在多层感知器模型中，将图像展开成一维向量输入到网络中，忽略了图像的位置和结构信息，而卷积神经网络能够更好的利用图像的结构信息。LeNet-5是一个较简单的卷积神经网络，图2显示了其结构：输入的二维图像，先经过两次卷积层到池化层，再经过全连接层，最后使用softmax分类作为输出层。

图2. LeNet-5卷积神经网络结构

操作过程

PaddlePaddle在API中提供了自动加载MNIST数据的模块paddle.dataset.mnist。加载后的数据位于/home/username/.cache/paddle/dataset/mnist下：

文件名称	说明
train-images-idx3-ubyte	训练数据图片，60,000条数据
train-labels-idx1-ubyte	训练数据标签，60,000条数据
t10k-images-idx3-ubyte	测试数据图片，10,000条数据
t10k-labels-idx1-ubyte	测试数据标签，10,000条数据

Fluid API 概述

Fluid API是最新的 PaddlePaddle API，它在不牺牲性能的情况下简化了模型配置，建议使用。

下面是 Fluid API 中几个重要概念的概述：

inference_program：指定如何从数据输入中获得预测的函数，这是指定网络流的地方。
train_program：指定如何从 inference_program 和标签值中获取 loss 的函数，这是指定损失计算的地方。
optimizer_func: 指定优化器配置的函数，优化器负责减少损失并驱动训练，Paddle 支持多种不同的优化器。

加载 PaddlePaddle 的 Fluid API 包。

import os
from PIL import Image # 导入图像处理模块
import matplotlib.pyplot as plt
import numpy
import paddle # 导入paddle模块
import paddle.fluid as fluid

Program Functions 配置

我们需要设置 inference_program 函数。下面演示三个不同的分类器，每个分类器都定义为 Python 函数。我们需要将图像数据输入到分类器中。Paddle 为读取数据提供了一个特殊的层 fluid.data 层。让我们创建一个数据层来读取图像并将其连接到分类网络。

Softmax回归：只通过一层简单的以softmax为激活函数的全连接层，就可以得到分类的结果。

def softmax_regression():
    """
    定义softmax分类器：
        一个以softmax为激活函数的全连接层
    Return:
        predict_image -- 分类的结果
    """
    # 输入的原始图像数据，大小为28*28*1
    img = fluid.data(name='img', shape=[None, 1, 28, 28], dtype='float32')
    # 以softmax为激活函数的全连接层，输出层的大小必须为数字的个数10
    predict = fluid.layers.fc(
        input=img, size=10, act='softmax')
    return predict

多层感知器：下面代码实现了一个含有两个隐藏层（即全连接层）的多层感知器。其中两个隐藏层的激活函数均采用ReLU，输出层的激活函数用Softmax。

def multilayer_perceptron():
    """
    定义多层感知机分类器：
        含有两个隐藏层（全连接层）的多层感知器
        其中前两个隐藏层的激活函数采用 ReLU，输出层的激活函数用 Softmax

    Return:
        predict_image -- 分类的结果
    """
    # 输入的原始图像数据，大小为28*28*1
    img = fluid.data(name='img', shape=[None, 1, 28, 28], dtype='float32')
    # 第一个全连接层，激活函数为ReLU
    hidden = fluid.layers.fc(input=img, size=200, act='relu')
    # 第二个全连接层，激活函数为ReLU
    hidden = fluid.layers.fc(input=hidden, size=200, act='relu')
    # 以softmax为激活函数的全连接输出层，输出层的大小必须为数字的个数10
    prediction = fluid.layers.fc(input=hidden, size=10, act='softmax')
    return prediction

卷积神经网络LeNet-5: 输入的二维图像，首先经过两次卷积层到池化层，再经过全连接层，最后使用以softmax为激活函数的全连接层作为输出层。

def convolutional_neural_network():
    """
    定义卷积神经网络分类器：
        输入的二维图像，经过两个卷积-池化层，使用以softmax为激活函数的全连接层作为输出层

    Return:
        predict -- 分类的结果
    """
    # 输入的原始图像数据，大小为28*28*1
    img = fluid.data(name='img', shape=[None, 1, 28, 28], dtype='float32')
    # 第一个卷积-池化层
    # 使用20个5*5的滤波器，池化大小为2，池化步长为2，激活函数为Relu
    conv_pool_1 = fluid.nets.simple_img_conv_pool(
        input=img,
        filter_size=5,
        num_filters=20,
        pool_size=2,
        pool_stride=2,
        act="relu")
    conv_pool_1 = fluid.layers.batch_norm(conv_pool_1)
    # 第二个卷积-池化层
    # 使用50个5*5的滤波器，池化大小为2，池化步长为2，激活函数为Relu
    conv_pool_2 = fluid.nets.simple_img_conv_pool(
        input=conv_pool_1,
        filter_size=5,
        num_filters=50,
        pool_size=2,
        pool_stride=2,
        act="relu")
    # 以softmax为激活函数的全连接输出层，输出层的大小必须为数字的个数10
    prediction = fluid.layers.fc(input=conv_pool_2, size=10, act='softmax')
    return prediction

Train Program 配置

然后我们需要设置训练程序 train_program。它首先从分类器中进行预测。在训练期间，它将从预测中计算 avg_cost。

注意: 训练程序应该返回一个数组，第一个返回参数必须是 avg_cost。训练器使用它来计算梯度。

请随意修改代码，测试 Softmax 回归 softmax_regression, MLP 和卷积神经网络 convolutional neural network 分类器之间的不同结果。

def train_program():
    """
    配置train_program

    Return:
        predict -- 分类的结果
        avg_cost -- 平均损失
        acc -- 分类的准确率

    """
    # 标签层，名称为label,对应输入图片的类别标签
    label = fluid.data(name='label', shape=[None, 1], dtype='int64')

    # predict = softmax_regression() # 取消注释将使用 Softmax回归
    # predict = multilayer_perceptron() # 取消注释将使用 多层感知器
    predict = convolutional_neural_network() # 取消注释将使用 LeNet5卷积神经网络

    # 使用类交叉熵函数计算predict和label之间的损失函数
    cost = fluid.layers.cross_entropy(input=predict, label=label)
    # 计算平均损失
    avg_cost = fluid.layers.mean(cost)
    # 计算分类准确率
    acc = fluid.layers.accuracy(input=predict, label=label)
    return predict, [avg_cost, acc]

Optimizer Function 配置

在下面的 Adam optimizer，learning_rate 是学习率，它的大小与网络的训练收敛速度有关系。

1 2	def optimizer_program(): return fluid.optimizer.Adam(learning_rate=0.001)

数据集 Feeders 配置

下一步，我们开始训练过程。paddle.dataset.mnist.train()和paddle.dataset.mnist.test()分别做训练和测试数据集。这两个函数各自返回一个reader——PaddlePaddle中的reader是一个Python函数，每次调用的时候返回一个Python yield generator。

下面shuffle是一个reader decorator，它接受一个reader A，返回另一个reader B。reader B 每次读入buffer_size条训练数据到一个buffer里，然后随机打乱其顺序，并且逐条输出。

batch是一个特殊的decorator，它的输入是一个reader，输出是一个batched reader。在PaddlePaddle里，一个reader每次yield一条训练数据，而一个batched reader每次yield一个minibatch。

# 一个minibatch中有64个数据
BATCH_SIZE = 64

# 每次读取训练集中的500个数据并随机打乱，传入batched reader中，batched reader 每次 yield 64个数据
train_reader = paddle.batch(
        paddle.reader.shuffle(
            paddle.dataset.mnist.train(), buf_size=500),
        batch_size=BATCH_SIZE)
# 读取测试集的数据，每次 yield 64个数据
test_reader = paddle.batch(
            paddle.dataset.mnist.test(), batch_size=BATCH_SIZE)

构建训练过程

现在，我们需要构建一个训练过程。将使用到前面定义的训练程序 train_program, place 和优化器 optimizer,并包含训练迭代、检查训练期间测试误差以及保存所需要用来预测的模型参数。

Event Handler 配置

我们可以在训练期间通过调用一个handler函数来监控训练进度。我们将在这里演示两个 event_handler 程序。请随意修改 Jupyter Notebook ，看看有什么不同。

event_handler 用来在训练过程中输出训练结果

1
2
3

def event_handler(pass_id, batch_id, cost):
    # 打印训练的中间结果，训练轮次，batch数，损失函数
    print("Pass %d, Batch %d, Cost %f" % (pass_id,batch_id, cost))

from paddle.utils.plot import Ploter

train_prompt = "Train cost"
test_prompt = "Test cost"
cost_ploter = Ploter(train_prompt, test_prompt)

# 将训练过程绘图表示
def event_handler_plot(ploter_title, step, cost):
    cost_ploter.append(ploter_title, step, cost)
    cost_ploter.plot()

event_handler_plot 可以用来在训练过程中画图如下：

开始训练

可以加入我们设置的 event_handler 和 data reader，然后就可以开始训练模型了。设置一些运行需要的参数，配置数据描述 feed_order 用于将数据目录映射到 train_program 创建一个反馈训练过程中误差的train_test

定义网络结构：

# 该模型运行在单个CPU上
use_cuda = True # 如想使用GPU，请设置为 True
place = fluid.CUDAPlace(0) if use_cuda else fluid.CPUPlace()

# 调用train_program 获取预测值，损失值，
prediction, [avg_loss, acc] = train_program()

# 输入的原始图像数据，名称为img，大小为28*28*1
# 标签层，名称为label,对应输入图片的类别标签
# 告知网络传入的数据分为两部分，第一部分是img值，第二部分是label值
feeder = fluid.DataFeeder(feed_list=['img', 'label'], place=place)

# 选择Adam优化器
optimizer = optimizer_program()
optimizer.minimize(avg_loss)

设置训练过程的超参：

PASS_NUM = 5 #训练5轮
epochs = [epoch_id for epoch_id in range(PASS_NUM)]

# 将模型参数存储在名为 save_dirname 的文件中
save_dirname = "recognize_digits.inference.model"

def train_test(train_test_program,
                   train_test_feed, train_test_reader):

    # 将分类准确率存储在acc_set中
    acc_set = []
    # 将平均损失存储在avg_loss_set中
    avg_loss_set = []
    # 将测试 reader yield 出的每一个数据传入网络中进行训练
    for test_data in train_test_reader():
        acc_np, avg_loss_np = exe.run(
            program=train_test_program,
            feed=train_test_feed.feed(test_data),
            fetch_list=[acc, avg_loss])
        acc_set.append(float(acc_np))
        avg_loss_set.append(float(avg_loss_np))
    # 获得测试数据上的准确率和损失值
    acc_val_mean = numpy.array(acc_set).mean()
    avg_loss_val_mean = numpy.array(avg_loss_set).mean()
    # 返回平均损失值，平均准确率
    return avg_loss_val_mean, acc_val_mean

创建执行器：

1 2	exe = fluid.Executor(place) exe.run(fluid.default_startup_program())

设置 main_program 和 test_program ：

1 2	main_program = fluid.default_main_program() test_program = fluid.default_main_program().clone(for_test=True)

开始训练：

lists = []
step = 0

for epoch_id in epochs:
    for step_id, data in enumerate(train_reader()):
        metrics = exe.run(main_program,
                          feed=feeder.feed(data),
                          fetch_list=[avg_loss, acc])
        if step % 10 == 0: #每训练100次 打印一次log
            event_handler_plot(train_prompt, step, metrics[0])
        step += 1

    # 测试每个epoch的分类效果
    avg_loss_val, acc_val = train_test(train_test_program=test_program,
                                      train_test_reader=test_reader,
                                      train_test_feed=feeder)

    event_handler_plot(test_prompt, step, metrics[0])

    lists.append((epoch_id, avg_loss_val, acc_val))

    # 保存训练好的模型参数用于预测
    if save_dirname is not None:
        fluid.io.save_inference_model(save_dirname,
                                      ["img"], [prediction], exe,
                                      model_filename=None,
                                      params_filename=None)

# 选择效果最好的pass
best = sorted(lists, key=lambda list: float(list[1]))[0]
print('Best pass is %s, testing Avgcost is %s' % (best[0], best[1]))
print('The classification accuracy is %.2f%%' % (float(best[2]) * 100))

训练之后，检查模型的预测准确度。用 MNIST 训练的时候，一般 softmax回归模型的分类准确率约为 92.34%，多层感知器为97.66%，卷积神经网络可以达到 99.20%。

注：在aistudio中ploter和print存在原生bug，取消print后ploter方可使用

应用模型

可以使用训练好的模型对手写体数字图片进行分类，下面程序展示了如何使用训练好的模型进行推断。

生成预测输入数据

infer_3.png 是数字 3 的一个示例图像。把它变成一个 numpy 数组以匹配数据feed格式。

def load_image(file):
    # 读取图片文件，并将它转成灰度图
    im = Image.open(file).convert('L')
    # 将输入图片调整为 28*28 的高质量图
    im = im.resize((28, 28), Image.ANTIALIAS)
    # 将图片转换为numpy
    im = numpy.array(im).reshape(1, 1, 28, 28).astype(numpy.float32)
    # 对数据作归一化处理
    im = im / 255.0 * 2.0 - 1.0
    return im

tensor_img = load_image('work/infer_3.png')

Inference 创建及预测

通过load_inference_model来设置网络和经过训练的参数。我们可以简单地插入在此之前定义的分类器。

inference_scope = fluid.core.Scope()
with fluid.scope_guard(inference_scope):
    # 使用 fluid.io.load_inference_model 获取 inference program desc,
    # feed_target_names 用于指定需要传入网络的变量名
    # fetch_targets 指定希望从网络中fetch出的变量名
    [inference_program, feed_target_names,
     fetch_targets] = fluid.io.load_inference_model(
     save_dirname, exe, None, None)

    # 将feed构建成字典 {feed_target_name: feed_target_data}
    # 结果将包含一个与fetch_targets对应的数据列表
    results = exe.run(inference_program,
                            feed={feed_target_names[0]: tensor_img},
                            fetch_list=fetch_targets)
    lab = numpy.argsort(results)

    # 打印 infer_3.png 这张图片的预测结果
    img=Image.open('work/infer_3.png')
    plt.imshow(img)
    print("Inference result of work/infer_3.png is: %d" % lab[0][0][-1])

Tags: 飞桨深度学习神经网络

← Python全栈工程师数据准备过程中如何创建虚拟变量 →

赏

使用支付宝打赏

使用微信打赏

若你觉得我的文章对你有帮助，欢迎点击上方按钮对我打赏

关注微信公众号，读文章、听课程，提升技能