来源：https://stackabuse.com/heap-sort-in-python/

作者：Olivera Popović

翻译：老齐

介绍

堆排序是高效排序算法的另一个例子，它的主要优点是，无论输入数据如何，它的最坏情况运行时间都是O(n*logn)。

顾名思义，堆排序在很大程度上依赖于堆数据结构——优先级队列的常见实现。

毫无疑问，堆排序是一种简单的排序算法，而且与其他简单实现相比，堆排序是更有效，也很常见。

堆排序

堆排序的工作原理是从堆逐个“移除”元素并将它们添加到已排序的数组里，在进一步解释和重新访问堆数据结构之前，我们应该了解堆排序本身的一些属性。

它是一种原地算法（译者注：in-place algorithm，多数翻译为“原地算法”，少数也翻译为“就地算法”。这种算法是使用小的、固定数量的额外内存空间来转换资料的算法。），意味着它需要恒定数量的内存，即所需内存不取决于初始数组本身的大小，而取决于存储该数组所需的内存。

例如，不需要原始数组的副本，也不需要递归和递归调用堆栈。最简单的堆排序实现通常使用第二个数组来存储排序后的值。我们将使用这种方法，因为它在代码中更直观、更易于实现，但它也是百分百的原地算法。

堆排序不稳定，意思是相等的值，并不会在同样的相对位次上。对于整数、字符串等这些基本类型，不会出现这类问题，但当我们对复杂类型的对象排序时，可能会遇到。

例如，假设我们有一个自定义类Person带有age和name属性，在一个数组中几个此类的实例对象，比如按顺序出现19岁的名叫“Mike”的人和一个19岁的名叫“David”的人。

如果我们决定按年龄对这些人进行排序，就不能在排序数组中保证“Mike”会出现在“David”之前，即使他们在初始数组中是按这个顺序出现的。“Mike”有可能出现在“David”之前，但不能保证百分之百如此。

堆数据结构

堆是计算机科学中最流行和最常用的一种数据结构——更不用说在软件工程面试中非常流行了。

我们将讨论跟踪最小元素（最小堆）的堆，但它们也可以很容易地实现对最大元素（最大堆）的跟踪。

简单地说，最小堆是一种基于树的数据结构，其中每个节点比其所有子节点都小。通常使用二叉树。堆有三个基本操作——delete_minimum()、get_minimum()和add()。

每次，你只能删除堆中的第一个元素，然后对其进行“重新排序”。在添加或删除元素后，堆对自己会“重新排序”，以便最小的元素始终处于第一个位置。

注意：这绝不意味着堆是排序的数组。每个节点都小于其子节点这一事实不足以保证整个堆是按升序排列的。

我们来看一个关于堆的例子：

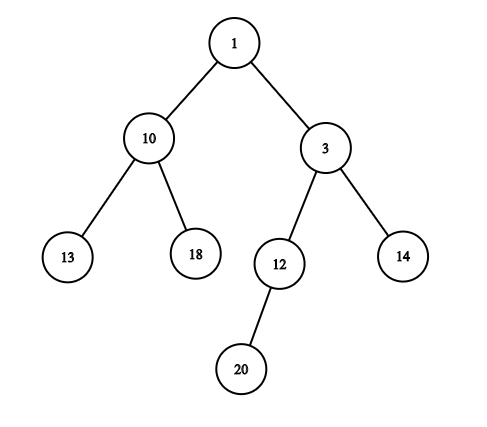
正如我们看到的，上面的例子确实符合堆的描述，但是没有排序。我们不会详细讨论堆实现，因为这不是本文的重点。当在堆排序中使用堆数据结构时，我们所利用的堆数据结构的关键优势是：下一个最小的元素始终是堆中的第一个元素。

实现

数组排序

译者注： 作者在本文中并没有严格区分Python中的列表和数组，而是将列表看做了数组，这对于列表中的元素是同一种类型的元素而言，无可厚非。对于排序，只有是同一种类型的元素，才有意义。

Python提供了创建和使用堆的方法，所以我们不必自己单独为了实现它们去写代码了:

• heappush(list, item)：向堆中添加一个元素，然后对其重新排序，使其保持堆状态。可用于空列表。
• heappop(list)：删除第一个（最小的）元素并返回该元素。此操作之后，堆仍然是一个堆，因此我们不必调用heapify()。
• heapify(list)：将给定的列表变成一个堆。

现在我们知道了这些，堆排序的实现就相当简单了：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

from heapq import heappop, heappush

def heap_sort(array):
    heap = []
    for element in array:
        heappush(heap, element)

    ordered = []

    # While we have elements left in the heap
    while heap:
        ordered.append(heappop(heap))

    return ordered

array = [13, 21, 15, 5, 26, 4, 17, 18, 24, 2]
print(heap_sort(array))

输出

1

[2, 4, 5, 13, 15, 17, 18, 21, 24, 26]

如我们所见，堆数据结构的繁重工作已经完成，我们所要做的只是添加所需的所有元素并逐个删除它们。它就像一台硬币计数机，根据输入的硬币的价值对它们进行分类，然后我们可以取出它们。

自定义对象排序

当使用自定义类时，事情会变得更加复杂。通常，为了使用我们的排序算法，建议不要重写类中的比较运算符，而是建议重写该算法，以便使用lambda函数比较。

但是，由于我们的实现依赖于内置堆方法，因此不能在这里这样做。

Python确实提供了以下方法：

• heapq.nlargest(*n*, *iterable*, *key=None*)：返回一个列表，其中包含由iterable定义的数据集中的n个最大元素。
• heapq.nsmallest(*n*, *iterable*, *key=None*)：返回一个列表，其中包含由iterable定义的数据集中的n个最小元素。

我们可以使用它来简单地获取n = len(array)最大/最小元素，但是方法本身不使用堆排序，本质上等同于只调用sorted()方法。

我们留给自定义类的唯一解决方案是实际重写比较运算符。遗憾的是，这使我们局限于对每个类只能进行一种比较。在我们的示例中，我们被局限于按年份对Movie对象进行排序。

但是，它确实让我们演示了在自定义类上使用堆排序。我们来定义Movie类：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

from heapq import heappop, heappush

class Movie:
    def __init__(self, title, year):
        self.title = title
        self.year = year

    def __str__(self):
        return str.format("Title: {}, Year: {}", self.title, self.year)

    def __lt__(self, other):
        return self.year < other.year

    def __gt__(self, other):
        return other.__lt__(self)

    def __eq__(self, other):
        return self.year == other.year

    def __ne__(self, other):
        return not self.__eq__(other)

现在，让我们稍微修改一下heap_sort()函数：

1
2
3
4
5
6
7
8
9
10
11

def heap_sort(array):
    heap = []
    for element in array:
        heappush(heap, element)

    ordered = []

    while heap:
        ordered.append(heappop(heap))

    return ordered

最后，让我们实例化一些电影，将它们放入一个数组中，然后对它们进行排序：

1
2
3
4
5
6
7
8
9
10

movie1 = Movie("Citizen Kane", 1941)
movie2 = Movie("Back to the Future", 1985)
movie3 = Movie("Forrest Gump", 1994)
movie4 = Movie("The Silence of the Lambs", 1991);
movie5 = Movie("Gia", 1998)

array = [movie1, movie2, movie3, movie4, movie5]

for movie in heap_sort(array):
    print(movie)

输出：

1
2
3
4
5

Title: Citizen Kane, Year: 1941
Title: Back to the Future, Year: 1985
Title: The Silence of the Lambs, Year: 1991
Title: Forrest Gump, Year: 1994
Title: Gia, Year: 1998

与其他排序算法的比较

堆排序被广泛使用，主要原因是它的可靠性，尽管它经常被运行良好的“快速排序”法所超越（译者注： 本文的微信公众号“老齐教室”以系列文章，介绍各种排序算法，并且用Python语言实现，敬请关注）。

堆排序的主要优点是时间复杂度上的O(n*logn)上限以及安全性。Linux内核开发人员给出了使用堆排序而不是快速排序的以下理由：

堆排序的平均排序时间和最坏排序时间均为O(n*logn)，虽然qsort的平均速度快了20%，但不得不容忍O(n*n)的最坏可能情形和额外的内存支出，这使它不太适合在操作系统内核中使用。

此外，快速排序算法法在可预测的情况下表现不佳。并且，如果对内部实现有足够的了解，你可能会意识到它造成的安全风险（主要是DDoS攻击），因为不良的O(n^2)行为很容易被触发。

经常被用来与堆排序比较的另一种算法是归并排序算法（译者注： 本微信公众号也会刊发相关文章给予介绍，敬请关注），它们具有相同的时间复杂度。

归并排序的优点是稳定、可并行运算，而堆排序两者都做不到。

另一个注意事项是：即使复杂度相同，堆排序在大多数情况下也比归并排序慢，因为堆排序具有较大的常数因子。

然而，堆排序比归并排序更容易实现，因此当内存比速度更重要时，它是首选。

结论

正如我们所看到的，堆排序不像其他高效的通用算法那么流行，但是它的可预测行为（而不是不稳定的行为）使它成为一个很好的算法，适用于内存和安全性比稍快的运行速度更重要的场合。

实现和利用Python提供的内置功能是非常直观的，我们实际上要做的就是将元素放在一个堆中并取出它们，就像对待硬币计数器一样。

关注微信公众号：老齐教室。读深度文章，得精湛技艺，享绚丽人生。