前面用小海龟绘制了一个多边形，这仅仅是对Python的初步了解，如果要更深入地研究如何用Python学习数学，还要继续学习有关运算。本节就向读者介绍Python中的基本算术运算。

下面的表格中显示了各种运算及其对应的符号。

如何使用？

还是打开IDLE，你会看到下面的界面——前面也肯定看到过了，不过那时候我们没有研究它。

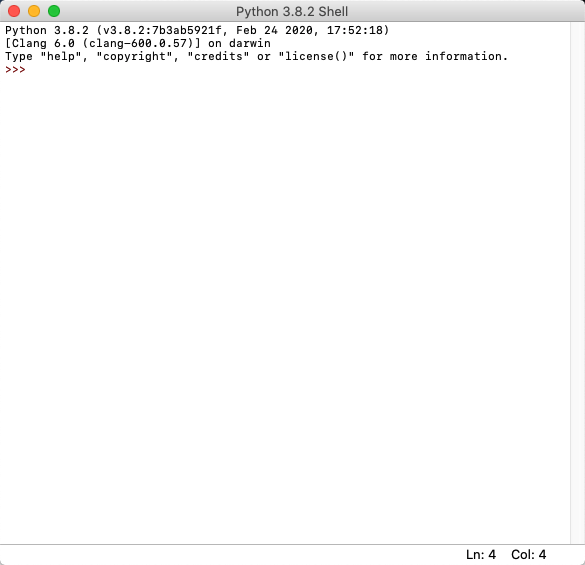
现在我们要使用这个界面进行操作了。在这个界面中，我们能够知道当前使用的Python版本——上图中演示使用的是3.8.2，读者的可以与此不同，但必须是3.x.x样式的版本，即Python3。此外，还看到了一个重要的提示符>>>，有这个提示符，表示当前的模式是“交互模式”，在此模式之下，当我们输入一条指令之后，敲回车，Python解析器就会对这条指令进行解析，然后返回该指令的结果。例如：

1
2

>>> 3 + 4
7

写了3 + 4之后，敲回车，就返回了7。

这就是交互模式的效果。

注意，在写3 + 4的时候，在3、+、4之间有空格，这里的空格并不被计入指令内容之中，只是为了显示“好看”。没有空格也可以，但是显示就不好看了。

在交互模式下，练习使用前面表格中的运算符：

1
2
3
4
5
6
7
8

>>> 5 - 9
-4
>>> 8 * 9
72
>>> 8 / 2
4.0
>>> 2 ** 5
32

此外，我们在前面曾经介绍过了变量，在交互模式中也可以继续使用。

1
2
3

>>> x = 5 - 9
>>> x
-4

从上面的练习中可以看出来，所谓交互模式，就是把.py文件中的每一句单独拿出来执行。

如果在交互模式下完成复杂的运算，比如四则混合运算，可以吗？

试一试：

1
2

>>> 3 + 3 * (4 - 2)
9

还是要提示，在输入上述所有内容的时候，一定要在英文状态下输入。

对于常见的数学运算，在Python中还有一些内置函数给予支持，比如：abs()、divmod()、pow()、round()、sum()，下面演示一下这几个内置函数的使用方法，从中可以了解它们的含义。

• abs()：求绝对值

1
2

>>> abs(-2)
2

abs()是对任何数求模——对于实数，就是绝对值，通常情况，我们讨论的数都是实数，于是就称其取绝对值。如果abs()的参数是一个复数，就是对其取模。

• divmod()：计算商和余数

1
2

>>> divmod(5, 2)
(2, 1)

divmod()的参数有两个，第一个是被除数，第二个是除数，返回结果是用圆括号包裹的一个对象，这个对象是Python中的一个内置对象，叫做元组。元组里面有两个数字，第一表示上面两个数相除得到的商，第二个表示的是余数。

特别提醒，如果被除数或除数是负数，在计算的时候，不同语言有不同的处理习惯，我们先来看一下Python中的计算结果：

1
2
3
4

>>> divmod(-5, 2)
(-3, 1)
>>> divmod(11, -5)
(-3, -4)

那么Python中是按照什么习惯规则计算的呢？有一个基本公式：

$$ (a // b) * b + (a%b) \equiv a$$

a、b分别表示被除数和除数，如果a / b，可以用//符号得到这两个数相除的商，我们也称这种相除为地板除，例如：

1
2
3
4
5
6

>>> 5 // 2
2
>>> -5 // 2
-3
>>> 11 // -5
-3

在上面的公式中，还出现了另外一种运算a % b，它表示的是计算这两数相除的余数。

1
2
3
4
5
6

>>> 5 % 2
1
>>> -5 % 2
1
>>> 11 % -5
-4

并且，在Python中，余数的符号和除数b的符号相同。

以上就是Python中计算商和余数的规则。

• pow()：幂函数

这个函数与前面介绍的运算符**的运算是等效的。

1
2
3
4

>>> 2 ** 3
8
>>> pow(2, 3)
8

• round()：实现四舍五入的函数

1
2
3
4

>>> round(3.1415, 2)
3.14
>>> round(2.345, 2)
2.35

• sum()：求和

1
2
3
4
5

>>> sum(1, 2)
Traceback (most recent call last):
  File "<pyshell#36>", line 1, in <module>
    sum(1,2)
TypeError: 'int' object is not iterable

像上面那样操作，试图计算1和2的和，但是报错了。因为这个函数不是这样使用的，它是用来计算一个序列——排成一列的数字就组成了一个序列——中所有数字的和，例如：

1
2
3

>>> lst = [1,2,3,4,5]
>>> sum(lst)
15

在这里，变量lst引用的对象是[1, 2, 3, 4, 5]，这个对象是用[ ]方括号包裹着，它是Python内置对象类型，称为列表。现在所创建的列表内，是一些数字。把这个列表作为sum()的参数，意思就是计算列表中所有数字的和。

用着方法，可以很容易地解决传说中高斯计算的那个题目：求1到100的所有整数的和。那就是写一个列表，其中的元素是1到100的整数，然后按照上面的方式调用sum()函数。只是，如果要真的写含有1到100的整数的列表，也够麻烦的。Python的最大特点就是帮助我们解决麻烦，它有一个内置函数：

1
2

>>> list(range(1, 101))
[1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42, 43, 44, 45, 46, 47, 48, 49, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63, 64, 65, 66, 67, 68, 69, 70, 71, 72, 73, 74, 75, 76, 77, 78, 79, 80, 81, 82, 83, 84, 85, 86, 87, 88, 89, 90, 91, 92, 93, 94, 95, 96, 97, 98, 99, 100]

对于range()应该不陌生吧，前面在画多边形的时候它也出现过了。这里我们再次使用它，能够轻松得到一个含有1到100所有整数的列表。于是乎：

1
2

>>> sum(range(1, 101))
5050

高斯的题目解决了！

专注于软件和AI的公众号

老齐教室